摘要：题设中两个主要条件是关于与的齐次式.而点.是函数图象上的两个点.是连接这两点的弦的斜率.若欲证的不等式关系也能转化为这样的斜率表示.则可以借助斜率进行“整体消元 .
网址：http://m.1010jiajiao.com/timu_id_198670[举报]
（1）已知k、n∈N*，且k≤n，求证：k
=n
；
（2）设数列a0，a1，a2，…满足a0≠a1，ai-1+ai+1=2ai（i=1，2，3，…）．证明：对任意的正整数n，p(x)=a0
(1-x)n+a1
x(1-x)n-1+a2
x2(1-x)n-2+…+an
xn是关于x的一次式．
查看习题详情和答案>>
| C | k n |
| C | k-1 n-1 |
（2）设数列a0，a1，a2，…满足a0≠a1，ai-1+ai+1=2ai（i=1，2，3，…）．证明：对任意的正整数n，p(x)=a0
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
（1）已知k、n∈N*，且k≤n，求证：
；
（2）设数列a，a1，a2，…满足a≠a1，ai-1+ai+1=2ai（i=1，2，3，…）．证明：对任意的正整数n，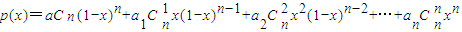
是关于x的一次式．
查看习题详情和答案>>
；（2）设数列a，a1，a2，…满足a≠a1，ai-1+ai+1=2ai（i=1，2，3，…）．证明：对任意的正整数n，
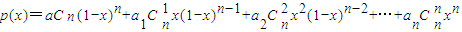是关于x的一次式．查看习题详情和答案>>
（1）已知k、n∈N*，且k≤n，求证：
；
（2）设数列a，a1，a2，…满足a≠a1，ai-1+ai+1=2ai（i=1，2，3，…）．证明：对任意的正整数n，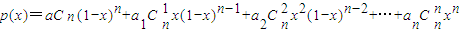
是关于x的一次式．
查看习题详情和答案>>
；（2）设数列a，a1，a2，…满足a≠a1，ai-1+ai+1=2ai（i=1，2，3，…）．证明：对任意的正整数n，
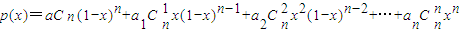是关于x的一次式．查看习题详情和答案>>
；
是关于x的一次式．