题目内容
(1)已知k、n∈N*,且k≤n,求证:k
=n
;
(2)设数列a0,a1,a2,…满足a0≠a1,ai-1+ai+1=2ai(i=1,2,3,…).证明:对任意的正整数n,p(x)=a0
(1-x)n+a1
x(1-x)n-1+a2
x2(1-x)n-2+…+an
xn是关于x的一次式.
| C | k n |
| C | k-1 n-1 |
(2)设数列a0,a1,a2,…满足a0≠a1,ai-1+ai+1=2ai(i=1,2,3,…).证明:对任意的正整数n,p(x)=a0
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
分析:(1)利用组合的阶乘公式,分别化简左、右边,即可得证;
(2)由题意得数列a0,a1,a2,…为等差数列,且公差为a1-a0≠0,利用p(x)=a0
(1-x)n+a1
x(1-x)n-1+a2
x2(1-x)n-2+…+an
xn=a0
(1-x)n+[a0+(a1-a0)]
x(1-x)n-1+…+[a0+n(a1-a0)]
xn,即可化简得到结论.
(2)由题意得数列a0,a1,a2,…为等差数列,且公差为a1-a0≠0,利用p(x)=a0
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | n n |
解答:证明:(1)左边=k
=k•
=
,
右边=n•
=
,
所以k
=n
;
(2)由题意得数列a0,a1,a2,…为等差数列,且公差为a1-a0≠0.
则p(x)=a0
(1-x)n+a1
x(1-x)n-1+a2
x2(1-x)n-2+…+an
xn=a0
(1-x)n+[a0+(a1-a0)]
x(1-x)n-1+…+[a0+n(a1-a0)]
xn=a0[
(1-x)n+
x(1-x)n-1+…+
xn]+(a1-a0)[
x(1-x)n-1+2
x2(1-x)n-2+…+n
xn]=a0[(1-x)+x]n+(a1-a0)nx[
(1-x)n-1+
x(1-x)n-2+…+
xn-1]=a0+(a1-a0)nx[x+(1-x)]n-1=a0+(a1-a0)nx,
所以对任意的正整数n,p(x)是关于x的一次式.
| C | k n |
| n! |
| k!(n-k)! |
| n! |
| (k-1)!(n-k)! |
右边=n•
| (n-1)! |
| (k-1)!(n-k)! |
| n! |
| (k-1)!(n-k)! |
所以k
| C | k n |
| C | k-1 n-1 |
(2)由题意得数列a0,a1,a2,…为等差数列,且公差为a1-a0≠0.
则p(x)=a0
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | n n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n-1 |
| C | 1 n-1 |
| C | n-1 n-1 |
所以对任意的正整数n,p(x)是关于x的一次式.
点评:本题主要考查组合数的性质、二项式定理,考查推理论证能力.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 ;
; 是关于x的一次式.
是关于x的一次式. ;
;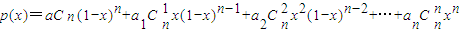 是关于x的一次式.
是关于x的一次式. ;
;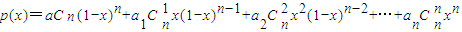 是关于x的一次式.
是关于x的一次式.