设函数y＝f(x)的定义域为R，对任意实数m，n，有f(m＋n)＝f(m)f(n)，且当x＜0时，f(x)＞1数列{a_n}满足a₁＝f(0)，且(n∈N^*)．

(1)求证：y＝f(x)在R上单调递减．

(2)求数列{a_n}的通项公式．

(3)是否存在正数k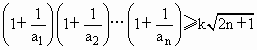，对一切n∈N^*均成立？若存在．试求出k的最大值并证明：若不存在，请说明理由．

设函数f(x)＝ax²＋lnx．

(Ⅰ)当a＝－1时，求函数y＝f(x)的单调区间和极大值点；

(Ⅱ)已知a＜0，若函数y＝f(x)的图象总在直线的下方，求a的取值范围；

(Ⅲ)记(x)为函数f(x)的导函数．若a＝1，试问：在区间[1，10]上是否存在k(k＜100)个正数x₁，x₂，x₃…x_k，使得(x₁)＋(x₂)＋(x₃)＋…＋(x_k)≥2010成立？请证明你的结论．

设函数f(x)的定义域为R，当x＞0时，f(x)＞1，且对任意x，y∈R，都有f(x＋y)＝f(x)·f(y)，且f(2)＝4．

(1)求f(0)，f(1)的值；

(2)证明：f(x)在R上为单调递增函数；

(3)若有不等式f(x)·f(1＋＜2)成立，求x的取值范围．

设函数f(x)为定义在R上的偶函数，当x＜－1时，y＝f(x)的图象是经过A(－2，0)、B(－3，－1)两点的一条射线，当－1≤x≤1时，y＝f(x)的图象是顶点在(0，)，对称轴是y轴，且过点(－1，1)的一段抛物线．

(1)试求函数y＝f(x)的解析式；

(2)画出f(x)的图象并写出其单调递增区间．

已知函数f(x)＝x²－2x－3与y＝－3在同一平面直角坐标系中的图象如图所示，记F(x)为“f(|x|)”与“－3”两者中的较小者，且当f(|x|)＝－3时，F(x)＝－3．有以下四种关于函数y＝F(x)的说法：

①F(4)＜F(－5)；

②F(－1)是y＝F(x)的最小值；

③方程F(x)＝0有两个实数根；

④y＝F(x)在(－∞，1)上单调递减．

其中真命题的个数为

A．0

B．1

C．2

D．3