摘要:对于任何都成立. 当且仅当时对于任何都成立.当时.的解集为
网址:http://m.1010jiajiao.com/timu_id_198134[举报]
已知等差数列![]() 中,公差
中,公差![]() ,其前
,其前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,
![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设由![]() (
(![]() )构成的新数列为
)构成的新数列为![]() ,求证:当且仅当
,求证:当且仅当![]() 时,数列
时,数列![]() 是等差数列;
是等差数列;
(3)对于(2)中的等差数列![]() ,设
,设![]() (
(![]() ),数列
),数列![]() 的前
的前
![]() 项和为
项和为![]() ,现有数列
,现有数列![]() ,
,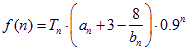 (
(![]() ),
),
是否存在整数![]() ,使
,使![]() 对一切
对一切![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的最小
的最小
值,若不存在,请说明理由.
查看习题详情和答案>>(本题满分16分)本题共有3个小题,第1小题满分各4分,第2、3小题满分各6分.
已知等差数列![]() 中,公差
中,公差![]() ,其前
,其前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设由![]() (
(![]() )构成的新数列为
)构成的新数列为![]() ,求证:当且仅当
,求证:当且仅当![]() 时,数列
时,数列![]() 是等差数列;
是等差数列;
(3)对于(2)中的等差数列![]() ,设
,设![]() (
(![]() ),数列
),数列![]() 的前
的前![]() 项和为
项和为![]() ,现有数列
,现有数列![]() ,
,![]() (
(![]() ),
),
求证:存在整数![]() ,使
,使![]() 对一切
对一切![]() 都成立,并求出
都成立,并求出![]() 的最小值.
的最小值.
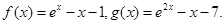
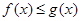 ;(4分)
;(4分)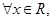 有
有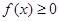 成立,当且仅当
成立,当且仅当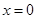 时取等号.由此结论证明:
时取等号.由此结论证明: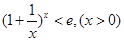 .(6分)
.(6分) (c≠0)构成的新数列为bn,求证:当且仅当
(c≠0)构成的新数列为bn,求证:当且仅当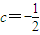 时,数列bn是等差数列;
时,数列bn是等差数列;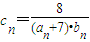 (n∈N*),数列cn的前n项和为Tn,现有数列f(n),
(n∈N*),数列cn的前n项和为Tn,现有数列f(n),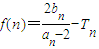 (n∈N*),
(n∈N*),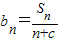 (c≠0)构成的新数列为bn,求证:当且仅当
(c≠0)构成的新数列为bn,求证:当且仅当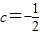 时,数列bn是等差数列;
时,数列bn是等差数列;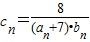 (n∈N*),数列cn的前n项和为Tn,现有数列f(n),
(n∈N*),数列cn的前n项和为Tn,现有数列f(n),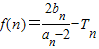 (n∈N*),
(n∈N*),