题目内容
已知等差数列![]() 中,公差
中,公差![]() ,其前
,其前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,
![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设由![]() (
(![]() )构成的新数列为
)构成的新数列为![]() ,求证:当且仅当
,求证:当且仅当![]() 时,数列
时,数列![]() 是等差数列;
是等差数列;
(3)对于(2)中的等差数列![]() ,设
,设![]() (
(![]() ),数列
),数列![]() 的前
的前
![]() 项和为
项和为![]() ,现有数列
,现有数列![]() ,
,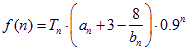 (
(![]() ),
),
是否存在整数![]() ,使
,使![]() 对一切
对一切![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的最小
的最小
值,若不存在,请说明理由.
(1)![]() (2)见解析
(2)见解析
(3)存在不小于13的整数,使![]() 对一切
对一切![]() 都成立,
都成立,![]()
解析:
(1)∵等差数列![]() 中,公差
中,公差![]() ,
,
∴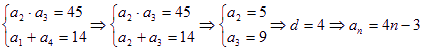 (4分)
(4分)
(2)![]() ,
,![]()
![]() , (6分)
, (6分)
由![]() 得
得![]() ,化简得
,化简得![]() ,∴
,∴![]() (8分)
(8分)
反之,令![]() ,即得
,即得![]() ,显然数列
,显然数列![]() 为等差数列,
为等差数列,
∴ 当且仅当![]() 时,数列
时,数列![]() 为等差数列. (10分)
为等差数列. (10分)
(3)![]()
![]()
∴![]()
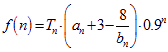
![]()
![]() (12分)
(12分)
![]()
![]()
![]()
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,∴
,∴![]() , (14分)
, (14分)
∴存在不小于13的整数,使![]() 对一切
对一切![]() 都成立,
都成立,![]() (16分)
(16分)

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
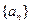 中,公差
中,公差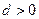 ,其前
,其前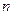 项和为
项和为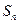 ,且满足
,且满足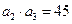 ,
,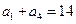 .
.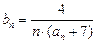 (
(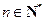 ),数列
),数列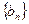 的前
的前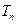 ,求证:
,求证: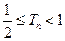 ;
;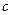 (
(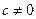 ),
),  使得数列
使得数列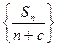 为等差数列?若存在,试求出
为等差数列?若存在,试求出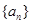 中,公差
中,公差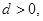 又
又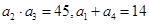 .
.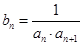 ,数列
,数列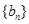 的前
的前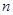 项和记为
项和记为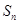 ,求
,求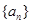 中,公差
中,公差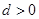 ,其前
,其前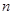 项和为
项和为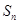 ,且满足
,且满足 ,
,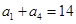 .
.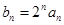 (
( ),求数列
),求数列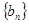 的前
的前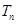 ;
;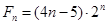 ,试比较
,试比较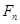 与
与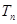 的大小.
的大小.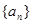 中,公差
中,公差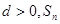 为其前n项和,且满足:
为其前n项和,且满足: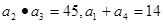 。
。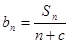 构造一个新的数列
构造一个新的数列 ,使
,使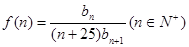 的最大值。
的最大值。