摘要:于是左边=.故原不等式获证.
网址:http://m.1010jiajiao.com/timu_id_198088[举报]
C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C.
对于函数y=ex,曲线y=ex在与坐标轴交点处的切线方程为y=x+1,由于曲线 y=ex在切线y=x+1的上方,故有不等式ex≥x+1.类比上述推理:对于函数y=lnx(x>0),有不等式( )
查看习题详情和答案>>
某同学在证明命题“
-
<
-
”时作了如下分析,请你补充完整.
要证明
-
<
-
,只需证明
+
<
+
+
<
+
,只需证明
展开得9+2
<9+2
,即
<
,只需证明14<18,
所以原不等式:
+
<
+
成立.
查看习题详情和答案>>
| 7 |
| 3 |
| 6 |
| 2 |
要证明
| 7 |
| 3 |
| 6 |
| 2 |
| 7 |
| 2 |
| 6 |
| 3 |
| 7 |
| 2 |
| 6 |
| 3 |
(
+
)2<(
+
)2
| 7 |
| 2 |
| 6 |
| 3 |
(
+
)2<(
+
)2
,| 7 |
| 2 |
| 6 |
| 3 |
展开得9+2
| 14 |
| 18 |
| 14 |
| 18 |
因为14<18显然成立
因为14<18显然成立
,所以原不等式:
| 7 |
| 2 |
| 6 |
| 3 |
阅读下面所给材料:已知数列{an},a1=2,an=3an-1+2,求数列的通项an.
解:令an=an-1=x,则有x=3x+2,所以x=-1,故原递推式an=3an-1+2可转化为:
an+1=3(an-1+1),因此数列{an+1}是首项为a1+1,公比为3的等比数列.
根据上述材料所给出提示,解答下列问题:
已知数列{an},a1=1,an=3an-1+4,
(1)求数列的通项an;并用解析几何中的有关思想方法来解释其原理;
(2)若记Sn=
,求
Sn;
(3)若数列{bn}满足:b1=10,bn+1=100bn3,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn. 查看习题详情和答案>>
解:令an=an-1=x,则有x=3x+2,所以x=-1,故原递推式an=3an-1+2可转化为:
an+1=3(an-1+1),因此数列{an+1}是首项为a1+1,公比为3的等比数列.
根据上述材料所给出提示,解答下列问题:
已知数列{an},a1=1,an=3an-1+4,
(1)求数列的通项an;并用解析几何中的有关思想方法来解释其原理;
(2)若记Sn=
| n |
 |
| k=1 |
| 1 |
| lg(ak+2)lg(ak+1+2) |
| lim |
| n→∞ |
(3)若数列{bn}满足:b1=10,bn+1=100bn3,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn. 查看习题详情和答案>>
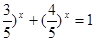 ”有如下思路;设
”有如下思路;设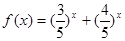 ,则
,则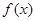 在R上单调递减,且
在R上单调递减,且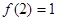 ,故原方程有唯一解x=2,类比上述解题思路,不等式
,故原方程有唯一解x=2,类比上述解题思路,不等式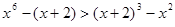 的解集是 .
的解集是 .