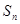网址:http://m.1010jiajiao.com/timu_id_19783[举报]
一、DBBCA,CCBCD,BA
二、13、3,14、,15、x+y-2=0,16、12
三、解答题:
17.解:∵……………2分 ………4分
…………………………………………6分
……………………………8分
………………………………………………10分
又 ∴………………………12分
18.解:(Ⅰ)记甲、乙、丙三台机器在一小时需要照顾分别为事件A、B、C,……1分
则A、B、C相互独立,
由题意得: P(AB)=P(A)?P(B)=0.05
P(AC)=P(A)?P(C)=0.1
P(BC)=P(B)?P(C)=0.125…………………………………………………………4分
解得:P(A)=0.2;P(B)=0.25;P(C)=0.5
所以, 甲、乙、丙每台机器在这个小时内需要照顾的概率分别是0.2、0.25、0.5……6分
(Ⅱ)∵A、B、C相互独立,∴相互独立,……………………………………7分
∴甲、乙、丙每台机器在这个小时内需都不需要照顾的概率为
…………………………10分
∴这个小时内至少有一台需要照顾的概率为
……12分
19.证明:(Ⅰ)作AD的中点O,则VO⊥底面
ABCD.…………………………1分
建立如图空间直角坐标系,并设正方形边长为1,…………………………2分
则A(,0,0),B(,1,0),C(-,1,0),D(-,0,0),V(0,0,),
∴………………………………3分
由……………………………………4分
……………………………………5分
又AB∩AV=A ∴AB⊥平面VAD…………………………………………6分
(Ⅱ)由(Ⅰ)得是面VAD的法向量………………………………7分
设是面VDB的法向量,则
……9分
∴,……………………………………11分
又由题意知,面VAD与面VDB所成的二面角,所以其大小为…………12分
20.解:由题意得:……………1分 即…………3分
又…………4分 又成等比数列,
∴该数列的公比为,………6分 所以………8分
又……………………………………10分
所以数列的通项为……………………………12分
21.解:设容器的高为x,容器的体积为V,……………………………………………1分
则V=(90-2x)(48-2x)x,(0<V<24)………………………………………………5分
=4x3-276x2+4320x ∵V′=12 x2-552x+4320………………………………7分
由V′=12 x2-552x+4320=0得x1=10,x2=36
∵x<10 时,V′>0, 10<x<36时,V′<0, x>36时,V′>0,
所以,当x=10,V有极大值V(10)=1960………………………………………10分
又V(0)=0,V(24)=0,………………………………………………………………11分
所以当x=10,V有最大值V(10)=1960……………………………………………12分
22.解:(Ⅰ)∵抛物线,即,
∴焦点为………………………………………………………1分
(1)直线的斜率不存在时,显然有………………………………3分
(2)直线的斜率存在时,设为k, 截距为b
即直线:y=kx+b 由已知得:
……………5分
……………7分
即的斜率存在时,不可能经过焦点……………………………………8分
所以当且仅当=0时,直线经过抛物线的焦点F…………………………9分
(Ⅱ)当时,
直线的斜率显然存在,设为:y=kx+b………………………………10分
则由(Ⅰ)得:
………………………11分
…………………………………………13分
所以直线的方程为,即………………14分
(本小题满分12分) 等差数列![]() 中,首项
中,首项![]() ,公差
,公差![]() ,前n项和为
,前n项和为![]() ,已知数列
,已知数列![]() 成等比数列,其中
成等比数列,其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .是否存在一个最小正整数M,使得当
.是否存在一个最小正整数M,使得当![]() 时,
时,![]() (
(![]() )恒成立?若存在,求出这个M值,若不存在,说明理由.
)恒成立?若存在,求出这个M值,若不存在,说明理由.
 和等比数列
和等比数列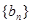 中,已知
中,已知 ,
,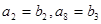 ;
;  和
和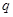 ;
;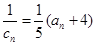 ,求数列
,求数列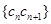 的前
的前 项和
项和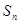
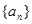 和等比数列
和等比数列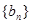 中,已知
中,已知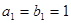 ,
,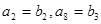 ;
; 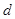 和
和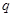 ;
;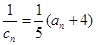 ,求数列
,求数列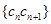 的前
的前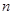 项和
项和