摘要：(II)证明:因为上为减函数.
网址：http://m.1010jiajiao.com/timu_id_193152[举报]
设f（x）是定义在R上的偶函数，其图象关于直线x=1对称，对任意x1，x2∈[0，
]，都有f（x1+x2）=f（x1）•f（x2），且f（1）=4．
（I） 求f(
)及f(
)；
（II） 证明f（x）是周期函数；
（Ⅲ）若对任意x∈[0，
]，都有f（x）＞1，证明函数f（x）在[0，
]上为增函数．
查看习题详情和答案>>
| 1 |
| 2 |
（I） 求f(
| 1 |
| 2 |
| 1 |
| 4 |
（II） 证明f（x）是周期函数；
（Ⅲ）若对任意x∈[0，
| 1 |
| 2 |
| 1 |
| 2 |
（2011•重庆三模）过曲线y=
上的一点Q0（0，2）作曲线的切线，交x轴于点P1，过P1作垂直于x轴的直线交曲线于Q1，过Q1作曲线的切线，交x轴于点P2；过P2作垂直于x轴的直线交曲线于Q2，过Q2作曲线的切线，交x轴于点P3；…如此继续下去得到点列：P1，P2，P3，…Pn，…，设Pn的横坐标为xn（n∈N*）
（I）试用n表示xn；
（II）证明：
+
+…+
＜
；
（III）证明：
＞
+
+
+…．
查看习题详情和答案>>
| 2 |
| x+1 |
（I）试用n表示xn；
（II）证明：
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
| 11 |
| 6 |
（III）证明：
| 1 |
| xn |
| 1 |
| xn+1 |
| 1 |
| xn+2 |
| 1 |
| xn+3 |
已知椭圆
+
=1(a＞b＞0)的两个焦点分别为F1（-1，0），F2（1，0），点P在椭圆上，且满足|PF1|=2|PF2|，∠PF1F2=30°，直线y=kx+m与圆x2+y2=
相切，与椭圆相交于A，B两点．
（I）求椭圆的方程；
（II）证明∠AOB为定值（O为坐标原点）．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| 5 |
（I）求椭圆的方程；
（II）证明∠AOB为定值（O为坐标原点）．
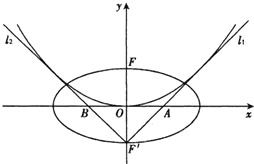已知椭圆E的中心在原点，焦点在x轴上，离心率为
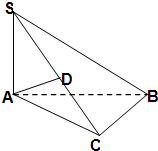如图，在三棱锥S-ABC中，BC⊥平面SAC，AD⊥SC．