题目内容
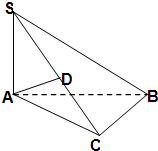 如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.
如图,在三棱锥S-ABC中,BC⊥平面SAC,AD⊥SC.(I)求证:AD⊥平面SBC;
(II)试在SB上找一点E,使得BC∥平面ADE,并证明你的结论.
分析:(I)通过证明BC⊥AD,通过AD⊥SC,BC∩SC=C,证明AD⊥平面SBC;
(II)过D作DE∥BC,交SB于E,E点即为所求.直接利用直线与平面平行的判定定理即可证明BC∥平面ADE.
(II)过D作DE∥BC,交SB于E,E点即为所求.直接利用直线与平面平行的判定定理即可证明BC∥平面ADE.
解答: 解:(I)证明:∵BC⊥平面SAC,AD?平面SAC,
解:(I)证明:∵BC⊥平面SAC,AD?平面SAC,
∴BC⊥AD,
又∵AD⊥SC,BC∩SC=C,BC?平面SBC,SC?平面SBC,
∴AD⊥平面SBC. …(5分)
(II)过D作DE∥BC,交SB于E,E点即为所求.
∵BC∥DE,BC?面ADE,DE?平面ADE,
∴BC∥平面ADE. …(10分)
 解:(I)证明:∵BC⊥平面SAC,AD?平面SAC,
解:(I)证明:∵BC⊥平面SAC,AD?平面SAC,∴BC⊥AD,
又∵AD⊥SC,BC∩SC=C,BC?平面SBC,SC?平面SBC,
∴AD⊥平面SBC. …(5分)
(II)过D作DE∥BC,交SB于E,E点即为所求.
∵BC∥DE,BC?面ADE,DE?平面ADE,
∴BC∥平面ADE. …(10分)
点评:本题考查直线与平面垂直,直线与平面平行的判定定理的应用,考查空间想象能力,逻辑推理能力.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC. 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( ) 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( ) (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )