摘要:所以.由于为正整数.所以.
网址:http://m.1010jiajiao.com/timu_id_193093[举报]
中国跳水运动员进行10m跳台跳水训练时,身体(看成一点)在空中的运动路线为如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面10
m,入水处距池边的距离为4m,同时,运动员在距水面高度为5m或5m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式.
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3
m,问此次跳水会不会失误?并通过计算说明理由.
(3)要使此次跳水不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多应为多少?

查看习题详情和答案>>
| 2 |
| 3 |
(1)求这条抛物线的解析式.
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3
| 3 |
| 5 |
(3)要使此次跳水不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多应为多少?

对于以下各命题:
(1)归纳推理特征是由部分到整体、特殊到一般;类比推理特征是由特殊到特殊;演绎推理特征是由一般到特殊.
(2)综合法是一种顺推法,由因导果;分析法是一种逆推法,执果索因.
(3)若i为虚数单位,则3+4i>1+4i;
(4)若复数z满足
=4,则它的对应点Z的轨迹是以(1,-2)为圆心,半径为4的圆.则其中所有正确的命题序号是
查看习题详情和答案>>
(1)归纳推理特征是由部分到整体、特殊到一般;类比推理特征是由特殊到特殊;演绎推理特征是由一般到特殊.
(2)综合法是一种顺推法,由因导果;分析法是一种逆推法,执果索因.
(3)若i为虚数单位,则3+4i>1+4i;
(4)若复数z满足
|
(1)(2)(4)
(1)(2)(4)
.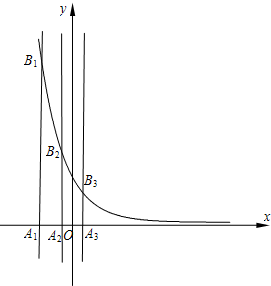 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理科做,文科不做)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.(参考数据:210=1024)
对于以下各命题:
(1)归纳推理特征是由部分到整体、特殊到一般;类比推理特征是由特殊到特殊;演绎推理特征是由一般到特殊.
(2)综合法是一种顺推法,由因导果;分析法是一种逆推法,执果索因.
(3)若i为虚数单位,则3+4i>1+4i;
(4)若复数z满足
=4,则它的对应点Z的轨迹是以(1,-2)为圆心,半径为4的圆.则其中所有正确的命题序号是______.
查看习题详情和答案>>
(1)归纳推理特征是由部分到整体、特殊到一般;类比推理特征是由特殊到特殊;演绎推理特征是由一般到特殊.
(2)综合法是一种顺推法,由因导果;分析法是一种逆推法,执果索因.
(3)若i为虚数单位,则3+4i>1+4i;
(4)若复数z满足
|
 (2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
(1)求证数列{sn}是公比绝对值小于1的等比数列;
(2)设{an}的公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3)(理)设{an}的公差d(d>0)为已知常数,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?并请说明理由.
(4)(文)设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.