��Ŀ����
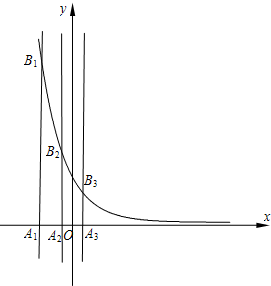 ��2006•������ģ����֪�Ȳ�����{an}������Ϊp������Ϊd��d��0�������ڲ�ͬ����Ȼ��n��ֱ��x=an��x���ָ������f(x)=(
��2006•������ģ����֪�Ȳ�����{an}������Ϊp������Ϊd��d��0�������ڲ�ͬ����Ȼ��n��ֱ��x=an��x���ָ������f(x)=(| 1 | 2 |
��1����֤����{sn}�ǹ��Ⱦ���ֵС��1�ĵȱ����У�
��2����{an}�Ĺ���d=1���Ƿ����������������n��������bn��bn+1��bn+2Ϊ�߳��������Σ�����˵�����ɣ�
��3�������������ĿƲ�������{an}�Ĺ���d=1���Ƿ����������ʵ��pʹ�ã�1��������ȱ�����{sn}����ĺ�S��2010��������ڣ�����һ������������pֵ����������ڣ���˵�����ɣ����ο����ݣ�210=1024��
��������1��an=p+��n-1��d��ֱ������AnAn+1Bn+1Bn�����׳���AnBn=f��an����An+1Bn+1=f��an+1������ΪAnAn+1 =d���������������ʽ��ʾ��sn�����õȱ����ж������֤�����ɣ�
��2��an=-1+��n-1��=n-2��bn=��
��n-2����bn��bn+1��bn+2Ϊ�߳��ܹ���һ�������Σ���bn+2+bn+1��bn����β���ʽ�����������
��4����������ȱ��������ʽ����S��2010 ����Ϊ S=
��2010��̽��p�Ĵ����ԣ�
��2��an=-1+��n-1��=n-2��bn=��
| 1 |
| 2 |
��4����������ȱ��������ʽ����S��2010 ����Ϊ S=
| 3 |
| 2p+1 |
����⣺��1���ɵȲ�����ͨ�ʽ�ɵ�an=p+��n-1��d��
bn=(
)an=(
)p+(n-1)d����2�֣�
sn=
[(
)p+(n-1)d+(
)p+nd]=
•(
)p•[(
)(n-1)d+(
)nd]��
����������Ȼ��n��
=
=
=(
)d��
��������{sn}�ǵȱ������ҹ���q=(
)d����Ϊd��0������|q|��1������5�֣�
���sn=
[(
)a1+nd+(
)a1+(n-1)d]=d•(1+2d)•(
)a1+1•(
)nd���ù���q=(
)dҲ�ɣ�
��2��an=p+��n-1��=n+p-1��bn=(
)n+p-1����ÿ��������n��bn��bn+1��bn+2
����bn��bn+1��bn+2Ϊ�߳��ܹ���һ�������Σ���bn+2+bn+1��bn��
��(
)n+p+1+(
)n+p��(
)n+p-1����n=-1����1+2��4�����Dz����ܵģ�
���Զ�ÿһ��������n����bn��bn+1��bn+2Ϊ�߳����ܹ��������Σ�����10�֣�
��3�������������ĿƲ�����s1=
��q=
����S=
=
�������pʹ��S=
��2010����2p��
=
����ȡ�����ã�p��-log21340��
��˷���������pֵ���ڣ�log21340��10.4����ȡp=-11�ȣ�����14�֣�
˵����ͨ�������pֵ����֤S=
��2010Ҳ�ɣ�
bn=(
| 1 |
| 2 |
| 1 |
| 2 |
sn=
| d |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| d |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
����������Ȼ��n��
| sn+1 |
| sn |
(
| ||||
(
|
1+(
| ||
| 2d+1 |
| 1 |
| 2 |
��������{sn}�ǵȱ������ҹ���q=(
| 1 |
| 2 |
���sn=
| d |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��2��an=p+��n-1��=n+p-1��bn=(
| 1 |
| 2 |
����bn��bn+1��bn+2Ϊ�߳��ܹ���һ�������Σ���bn+2+bn+1��bn��
��(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
���Զ�ÿһ��������n����bn��bn+1��bn+2Ϊ�߳����ܹ��������Σ�����10�֣�
��3�������������ĿƲ�����s1=
| 3 |
| 22+p |
| 1 |
| 2 |
| s1 |
| 1-q |
| 3 |
| 2p+1 |
�������pʹ��S=
| 3 |
| 2p+1 |
| 3 |
| 4020 |
| 1 |
| 1340 |
����ȡ�����ã�p��-log21340��
��˷���������pֵ���ڣ�log21340��10.4����ȡp=-11�ȣ�����14�֣�
˵����ͨ�������pֵ����֤S=
| 3 |
| 2p+1 |
�����������Ǻ��������С�����ʽ�Ľ�ϣ�����ȱ����е��ж�������������ʽ������ۣ��������������⣬���㣬��˼ά������

��ϰ��ϵ�д�
 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
�����Ŀ
 ��2006•������ģ����ͼ����������ABCD-A1B1C1D1�У�E����A1D1���е㣬HΪƽ��EDB
��2006•������ģ����ͼ����������ABCD-A1B1C1D1�У�E����A1D1���е㣬HΪƽ��EDB