摘要:A. B. C. D.答案:A
网址:http://m.1010jiajiao.com/timu_id_191509[举报]
解析:A错误.如图①所示,由两个结构相同的三棱锥叠放在一起构![]() 成的几何体,各面都是三角形,但它不是棱锥.B错误.如答图②③所示,若△ABC不是直角三角形,或是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥.C错误.若六棱锥的所有棱都相等,则底面多边形是正六边形.由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.D正确.
成的几何体,各面都是三角形,但它不是棱锥.B错误.如答图②③所示,若△ABC不是直角三角形,或是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥.C错误.若六棱锥的所有棱都相等,则底面多边形是正六边形.由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.D正确.

答案:D
查看习题详情和答案>> 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}(1)将“特征数”是{0,
| ||
| 3 |
y=
x-1
| ||
| 3 |
y=
x-1
; (答案写在答卷上)
| ||
| 3 |
(2)在(1)中,平移前后的两个函数分别与y轴交于A、B两点,与直线x=
| 3 |
(3)若(2)中的四边形与“特征数”是{1,-2b,b2+
| 1 |
| 2 |
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}
(1)将“特征数”是{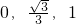 }的函数图象向下平移2个单位,得到的新函数的解析式是________; (答案写在答卷上)
}的函数图象向下平移2个单位,得到的新函数的解析式是________; (答案写在答卷上)
(2)在(1)中,平移前后的两个函数分别与y轴交于A、B两点,与直线x= 分别交于D、C两点,在平面直角坐标系中画出图形,判断以点A、B、C、D为顶点的四边形形状,并说明理由;
分别交于D、C两点,在平面直角坐标系中画出图形,判断以点A、B、C、D为顶点的四边形形状,并说明理由;
(3)若(2)中的四边形与“特征数”是{ }的函数图象的有交点,求满足条件的实数b的取值范围.
}的函数图象的有交点,求满足条件的实数b的取值范围.
查看习题详情和答案>>
铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2排放量b及每万吨铁矿石的价格c如下表:
某冶炼厂至少要生产1.9(万吨)贴,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为( )
A.14百万元
B.15百万元
C.20百万元
D.以上答案都不对
查看习题详情和答案>>
| a | b(万吨) | c(百万元) | |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
A.14百万元
B.15百万元
C.20百万元
D.以上答案都不对
查看习题详情和答案>>
铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2排放量b及每万吨铁矿石的价格c如下表:
某冶炼厂至少要生产1.9(万吨)贴,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为( )
A.14百万元
B.15百万元
C.20百万元
D.以上答案都不对
查看习题详情和答案>>
| a | b(万吨) | c(百万元) | |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
A.14百万元
B.15百万元
C.20百万元
D.以上答案都不对
查看习题详情和答案>>