网址:http://m.1010jiajiao.com/timu_id_185875[举报]
选择题(60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D.
A
C
A
B
B
A
C
A
C
B
填空题(16分)
13  14
14  15
15  16 8
16 8
17解:(1)由已知得, ………………6分
………………6分
(2) ………10分
………10分
=- ………12分
………12分
18解:(Ⅰ)(法一)f(x)的定义域为R。

 ,
,
所以f(x)在 上单调递增,在
上单调递增,在 上单调递减。……4分
上单调递减。……4分
所以f(x)值域为 ……6分
……6分
(法二) ……4分
……4分
所以f(x)的值域是 ………6分
………6分
(法三)由绝对值的几何意义知f(x)= 表示数轴上点P(x)到点M(2)与点N(-2)距离之和.……4分
表示数轴上点P(x)到点M(2)与点N(-2)距离之和.……4分
所以f(x)的值域是 .……6分
.……6分
(Ⅱ)原不等式等价于:
① 或②
或② 或③
或③ ……11分
……11分
所以原不等式解集为 ……12分
……12分
 19 解:设
19 解:设 ,由题意知
,由题意知 ,
, ……6分
……6分
又
所以双曲线方程为 ……10分
……10分
所以双曲线的渐近线方程为 ……12分
……12分
20解:(Ⅰ)由题意知方程 的两根是
的两根是
 ……4分
……4分
(Ⅱ)
 在[-1,2]上恒成立,………6分
在[-1,2]上恒成立,………6分
令
 ……8分
……8分
当x在[-1,2]上变化时, 的变化情况如下:
的变化情况如下:
x
-1



1
(1,2)
2

+
-
+
g(x)

ㄊ
极大值

ㄋ
极小值

ㄊ
2
所以当x=2时, ,
,
所以c的取值范围为 ……12分
……12分
21解:(1)当n=1时, ,当
,当 时,由
时,由 得
得 所以
所以 …………4分
…………4分
所以数列 是首项为3,公差为1的等差数列,
是首项为3,公差为1的等差数列,
所以数列 的通项公式为
的通项公式为 …………6分
…………6分
(2)
 22解 :(Ⅰ)由题设a=2,c=1从而
22解 :(Ⅰ)由题设a=2,c=1从而 所以椭圆的方程为:
所以椭圆的方程为:  ………5分
………5分
(Ⅱ)由题意得F(1,0),N(4,0),设A(m,n)
则B(m,-n)( ①
①
设动点M(x,y).AF与BN的方程分别为:n(x-1)-(m-1)y=0 ② n(x-4)+(m-4)y=0 ③
由②③得:当 时,
时, 代入①得
代入①得
当 时,由②③得:
时,由②③得: ,解得n=0,y=0与
,解得n=0,y=0与 矛盾,所以的轨迹方程为
矛盾,所以的轨迹方程为 。…………9分
。…………9分
(Ⅲ)△AMN的面积为△AFN与△MFN面积之和,且有相同的底边FN,当两高之和最大时,面积最大,这时AM应为特殊位置,所以猜想:当AM与x轴垂直时,△AMN的面积最大,|AM|=3,|FN|=3,这时 ,△AMN的面积最大最大值为
,△AMN的面积最大最大值为 ………11分。
………11分。
证明如下:设AM的方程为x=ty+1,代入 得
得
设A ,则有
,则有
令 ,则
,则
因为 ,所以
,所以 ,即
,即 时
时 有最大值3,△AMN的面积有
有最大值3,△AMN的面积有 最大值
最大值 。……13分
。……13分



⑴求数列
 的通项公式;
的通项公式;⑵设
 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;⑶是否存在以
 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
 的通项公式为
的通项公式为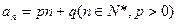 。数列
。数列 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。