摘要:(2)假设存在直线交椭圆于两点.且恰为的垂心.则
网址:http://m.1010jiajiao.com/timu_id_183618[举报]
已知椭圆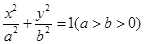 的右焦点为
的右焦点为 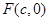 ,
, 为椭圆的上顶点,
为椭圆的上顶点,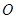 为坐标原点,且两焦点和短轴的两端构成边长为
为坐标原点,且两焦点和短轴的两端构成边长为 的正方形.
的正方形.
(1)求椭圆的标准方程;
(2)是否存在直线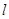 交与椭圆于
交与椭圆于 ,
,
 ,且使
,且使 ,使得
,使得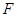 为
为 的垂心,若存在,求出
的垂心,若存在,求出 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看习题详情和答案>>
已知椭圆C:
+
=1,直线l与椭圆C交于A,B两不同的点.P为弦AB的中点.
(1)若直线l的斜率为
,求点P的轨迹方程.
(2)是否存在直线l,使得弦AB恰好被点(
,-
)平分?若存在,求出直线l的方程,若不存在,说明理由.
查看习题详情和答案>>
| x2 |
| 25 |
| y2 |
| 9 |
(1)若直线l的斜率为
| 4 |
| 5 |
(2)是否存在直线l,使得弦AB恰好被点(
| 4 |
| 3 |
| 3 |
| 5 |
已知圆C:x2+y2-2x-4y-3=0,直线l:y=x+b.
(1)若直线l与圆C相切,求实数b的值
(2)是否存在直线l与圆C交于A、B两点,且OA⊥OB(O为坐标原点);如果存在,求出直线l的方程,如果不存在,请说明理由. 查看习题详情和答案>>
(1)若直线l与圆C相切,求实数b的值
(2)是否存在直线l与圆C交于A、B两点,且OA⊥OB(O为坐标原点);如果存在,求出直线l的方程,如果不存在,请说明理由. 查看习题详情和答案>>