摘要：解:(1)由.可得由射影定理.得 在Rt△MOQ中.

网址：http://m.1010jiajiao.com/timu_id_183453[举报]

已知是公差为d的等差数列，是公比为q的等比数列

（Ⅰ）若 ，是否存在，有？请说明理由；

（Ⅱ）若（a、q为常数，且aq0）对任意m存在k，有，试求a、q满足的充要条件；

（Ⅲ）若试确定所有的p,使数列中存在某个连续p项的和式数列中的一项，请证明.

【解析】第一问中，由得，整理后，可得、，为整数不存在、，使等式成立。

（2）中当时，则

即，其中是大于等于的整数

反之当时，其中是大于等于的整数，则，

显然，其中

、满足的充要条件是，其中是大于等于的整数

（3）中设当为偶数时，式左边为偶数，右边为奇数，

当为偶数时，式不成立。由式得，整理

当时，符合题意。当，为奇数时，

结合二项式定理得到结论。

解（1）由得，整理后，可得、，为整数不存在、，使等式成立。

（2）当时，则即，其中是大于等于的整数反之当时，其中是大于等于的整数，则，

显然，其中

、满足的充要条件是，其中是大于等于的整数

（3）设当为偶数时，式左边为偶数，右边为奇数，

当为偶数时，式不成立。由式得，整理

当时，符合题意。当，为奇数时，

   由，得

当为奇数时，此时，一定有和使上式一定成立。当为奇数时，命题都成立

 

 查看习题详情和答案>>
我们常用构造等式对同一个量算两次的方法来证明组合恒等式，如由等式（1+x）2n=（1+x）n（1+x）n可得，左边xn的系数为
C
n
2n
，而右边(1+x)n(1+x)n=(
C
0
n
+
C
1
n
x+
C
2
n
x2+…+
C
n
n
xn)(
C
0
n
+
C
1
n
x+
C
2
n
x2+…+
C
n
n
xn)，xn的系数为
C
0
n
C
n
n
+
C
1
n
C
n-1
n
+
C
2
n
C
n-2
n
+…+
C
n
n
C
0
n
=(
C
0
n
)2+(
C
1
n
)2+(
C
2
n
)2+…+(
C
n
n
)2，由（1+x）2n=（1+x）n（1+x）n恒成立，可得(
C
0
n
)2+(
C
1
n
)2+(
C
2
n
)2+…+(
C
n
n
)2=
C
n
2n
．
利用上述方法，化简(
C
0
2n
)2-(
C
1
2n
)2+(
C
2
2n
)2-(
C
3
2n
)2+…+(
C
2n
2n
)2=
(-1)n
C
n
2n
(-1)n
C
n
2n
．
 查看习题详情和答案>>

设函数f（x）=在[1，+∞上为增函数.  

（1）求正实数a的取值范围；

（2）比较的大小，说明理由；

（3）求证：（n∈N*, n≥2）

【解析】第一问中，利用

解:（1）由已知：，依题意得：≥0对x∈[1，+∞恒成立

∴ax－1≥0对x∈[1，+∞恒成立    ∴a－1≥0即：a≥1

（2）∵a=1   ∴由（1）知：f（x）=在[1，+∞)上为增函数，

∴n≥2时：f（）=

  

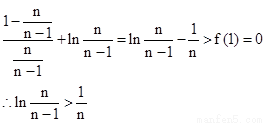
 (3)  ∵   ∴

 

 查看习题详情和答案>>
已知向量
a
=(4，3)，
b
=(-1，2)，若向量
a
+k
b
与
a
-
b
垂直，则k的值为（　　）
A．
23
3
B．7 下列人类所需的营养物质中，既不参与构成人体细胞，也不为人体提供能量的是，答案：0，选项：维生素，选项：水，选项：无机盐，... - 初中生物 - 精英家教网 .artpreview dt{background:#fff;color:#000}#cont{background:#fff url(http://img.jyeoo.net/images/body_bg.jpg) repeat-x;margin:0} function initJavaScriptCallback() { QuesCart.init("bio", true); } var imageRootUrl="http://img.jyeoo.net/",wwwRootUrl="http://www.jyeoo.com/",blogRootUrl="http://blog.jyeoo.com/",spaceRootUrl="http://space.jyeoo.com/",loginUrl="http://www.jyeoo.com/",logoutUrl="http://www.jyeoo.com/account/logoff",scriptsUrl="http://img.jyeoo.net/scripts/",isMobile=false;var mustyleAttr={color:"#000000",fontsize:"13px",fontfamily:"arial",displaystyle:"true"};document.domain="jyeoo.com";$.ajaxSetup({cache:true});C．-
11
5
D．-
23
3
考点：数量积判断两个平面向量的垂直关系．专题：计算题．分析：根据向量坐标运算的公式，结合
a
=(4，3)，
b
=(-1，2)，可得向量
a
+k
b
与
a
-
b
的坐标．再根据向量
a
+k
b
与
a
-
b
互相垂直，得到它们的数量积等于0，利用两个向量数量积的坐标表达式列方程，解之可得k的值．∵
a
=(4，3)，
b
=(-1，2)∴
a
+k
b
=（4-k，3+2k），
a
-
b
=（5，1）∵向量
a
+k
b
与
a
-
initJavaScript(); 充值|设为首页|免费注册|登录
输入公式
在线问答在线组卷在线训练 精英家教网 更多试题 》试题下列人类所需的营养物质中，既不参与构成人体细胞，也不为人体提供能量的是（　　）
A．维生素B．水C．无机盐D．脂肪
考点：人体需要的主要营养物质．分析：食物中含有六大类营养物质：蛋白质、糖类、脂肪、维生素、水和无机盐，每一类营养物质都是人体所必需的．食物所含的六类营养物质中，能为人体提供能量的是糖类、脂肪和蛋白质，同时这三类物质也是组织细胞的组成成分，水、无机盐和维生素不能为人体提供能量．其中糖类是最主要的供能物质，人体进行各项生命活动所消耗的能量主要来自于糖类的氧化分解，约占人体能量供应量的70%．脂肪也是重要的供能物质，但是人体内的大部分脂肪作为备用能源贮存在皮下等处，属于贮备能源物质．蛋白质也能为生命活动提供一部分能量，但蛋白质主要是构成组织细胞的基本物质，是人体生长发育、组织更新的重要原料，也是生命活动的调节等的物质基础．维生素属于有机物，但它既不能为人体提供能量，也不参与人体组织的构成，但它对人体的生命活动具有重要的调节作用．水和无机盐属于无机物．其中水既是人体重要的构成成分，也是人体各项生命活动进行的载体．无机盐也参与构成人体细胞．
故选：A点评：解答此题的关键是熟练掌握人体需要的营养物质及其作用．答题：xushifeng老师 隐藏解析在线训练
 查看习题详情和答案>>
我们常用构造等式对同一个量算两次的方法来证明组合恒等式，如由等式（1+x）2n=（1+x）n（1+x）n可得，左边xn的系数为
Cn2n
，而右边(1+x)n(1+x)n=(
C0n
+
C1n
x+
C2n
x2+…+
Cnn
xn)(
C0n
+
C1n
x+
C2n
x2+…+
Cnn
xn)，xn的系数为
C0n
Cnn
+
C1n
Cn-1n
+
C2n
Cn-2n
+…+
Cnn
C0n
=(
C0n
)2+(
C1n
)2+(
C2n
)2+…+(
Cnn
)2，由（1+x）2n=（1+x）n（1+x）n恒成立，可得(
C0n
)2+(
C1n
)2+(
C2n
)2+…+(
Cnn
)2=
Cn2n
．
利用上述方法，化简(
C02n
)2-(
C12n
)2+(
C22n
)2-(
C32n
)2+…+(
C2n2n
)2=______．
 查看习题详情和答案>>

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网