题目内容
我们常用构造等式对同一个量算两次的方法来证明组合恒等式,如由等式(1+x)2n=(1+x)n(1+x)n可得,左边xn的系数为
,而右边(1+x)n(1+x)n=(
+
x+
x2+…+
xn)(
+
x+
x2+…+
xn),xn的系数为
+
+
+…+
=(
)2+(
)2+(
)2+…+(
)2,由(1+x)2n=(1+x)n(1+x)n恒成立,可得(
)2+(
)2+(
)2+…+(
)2=
.
利用上述方法,化简(
)2-(
)2+(
)2-(
)2+…+(
)2=
| C | n 2n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | n n |
| C | 1 n |
| C | n-1 n |
| C | 2 n |
| C | n-2 n |
| C | n n |
| C | 0 n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | n 2n |
利用上述方法,化简(
| C | 0 2n |
| C | 1 2n |
| C | 2 2n |
| C | 3 2n |
| C | 2n 2n |
(-1)n
| C | n 2n |
(-1)n
.| C | n 2n |
分析:根据题意,构造等式(x-1)2n•(x+1)2n=(x2-1)2n,分别从等式的左边和等式的右边求得x2n的系数,令其相等,即可求得原式的值.
解答:解:根据题意,构造等式(x-1)2n•(x+1)2n=(x2-1)2n,
由等式的左边可得x2n的系数为C2n2n•(-1)2nC2n0+C2n2n-1•(-1)2n-1C2n1+C2n2n-2•(-1)2n-2C2n2+…+C2n0•(-1)0C2n2n,
即(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2,
由右等式的右端可得 x2n的系数为(-1)nC2nn,
故有(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn,
故答案为(-1)nC2nn.
由等式的左边可得x2n的系数为C2n2n•(-1)2nC2n0+C2n2n-1•(-1)2n-1C2n1+C2n2n-2•(-1)2n-2C2n2+…+C2n0•(-1)0C2n2n,
即(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2,
由右等式的右端可得 x2n的系数为(-1)nC2nn,
故有(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn,
故答案为(-1)nC2nn.
点评:本题考查组合数公式的应用,涉及二项式定理的应用,关键要根据题意,充分利用组合数的性质,属于中档题.

练习册系列答案
相关题目

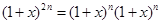 可得,左边
可得,左边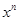 的系数为
的系数为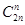 ,
,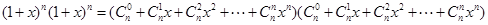 ,
, 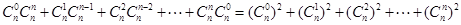 ,
,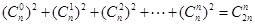 .
.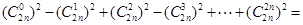 .
.