摘要：∴∠PAB为钝角时点A的坐标的取值范围为-----12分
网址：http://m.1010jiajiao.com/timu_id_183094[举报]
21．抛物线C的方程为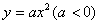
，过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)、B(x2,y2)两点(P,A,B三点互不相同)，且满足
.
，过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)、B(x2,y2)两点(P,A,B三点互不相同)，且满足.（Ⅰ）求抛物线C的焦点坐标和准线方程；
（Ⅱ）设直线AB上一点M，满足
，证明线段PM的中点在y轴上；
（Ⅲ）当
=1时，若点P的坐标为（1，－1），求∠PAB为钝角时点A的纵坐标
的取值范围.
抛物线C的方程为y=ax2(a＜0),过抛物线C上一点P(x0,y0)(x0≠0)作斜率为k1、k2的两条直线分别交抛物线C于A(x1,y1)、B(x2,y2)两点(P、A、B三点互不相同),且满足k2+λk1=0(λ≠0且λ≠-1).
(1)求抛物线C的焦点坐标和准线方程;
(2)设直线AB上一点M,满足
,证明线段PM的中点在y轴上;
(3)当λ=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标y1的取值范围.
查看习题详情和答案>>
抛物线C的方程为y=ax2(a＜0),过抛物线C上一点P(x0,y0)(x0≠0)作斜率分别为k1、k2的两条直线交抛物线C于A(x1,y1)、B(x2,y2)两点(P、A、B三点互不相同),且满足k2+λk1=0(λ≠0且λ≠-1).
(1)求抛物线C的焦点坐标和准线方程;
(2)设直线AB上一点M满足
=λ
,证明线段PM的中点在y轴上;
(3)当λ=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标y1的取值范围.
查看习题详情和答案>>
，过抛物线C上一点 
(
)作斜率为
的两条直线分别交抛物线C于
，
两点（P、A、B三点互不相同），且满足
（
≠0且
）。
，证明线段PM的中点在y轴上
时，若点P的坐标为（1，
1），求∠PAB为钝角时点A的纵坐标
的取值范围。