题目内容
抛物线C的方程为y=ax2(a＜0),过抛物线C上一点P(x0,y0)(x0≠0)作斜率分别为k1、k2的两条直线交抛物线C于A(x1,y1)、B(x2,y2)两点(P、A、B三点互不相同),且满足k2+λk1=0(λ≠0且λ≠-1).(1)求抛物线C的焦点坐标和准线方程;
(2)设直线AB上一点M满足
=λ
,证明线段PM的中点在y轴上;
(3)当λ=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标y1的取值范围.
(1)解：由抛物线C的方程y=ax2(a＜0＝,得焦点坐标为(0,),准线方程为y=-.
(2)证明：设直线PA的方程为y-y0=k1(x-x0),直线PB的方程为y-y0=k2(x-x0).
点P(x0,y0)和点A(x1,y1)的坐标是方程组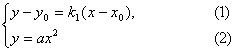
的解,将（2）代入（1）得ax2-k1x+k1x0-y0=0,于是x1+x0=
,x1=
-x0 (3)
又点P(x0,y0)和点B(x2,y2)的坐标是方程组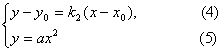
的解.将（5）代入（4）得ax2-k2x+k2x0-y0=0,于是x2+x0=
,x2=
-x0.（6）
由已知k2=-λk1,
则x2=-
-x0.
设点M的坐标为(xM,yM),由
=λ
,则
xM=
=
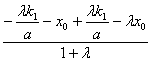=-x0.∴xM+x0=0,即线段PM的中点在y轴上.
(3)解：∵点P(1,-1)在抛物线y=ax2上,∴a=-1,抛物线的方程为y=-x2.
由（3）式知x1=-k1-1,代入y=-x2得y1=-(k1+1)2.
将λ=1代入（6）式得x2=k1-1,代入y=-x2得y2=-(k1-1)2.
∴A(-k1-1,-k12-2k1-1)、B(k1-1,-k12+2k1-1).
于是
=(k1+2,k12+2k1),
=(2k1,4k1).
·
=2k1(k1+2)+4k1(k12+2k1)=2k1(k1+2)(2k1+1).
∵∠PAB为钝角且P、A、B三点互不相同,故
·
＜0,即2k1(k1+2)(2k1+1)＜0.
∴k1＜-2或-
＜k1＜0.
又点A的纵坐标y1满足y1=-(k1+1)2,故
当k1＜-2时,y1＜-1;
当-
＜k1＜0时,-1＜y1＜-
.
∴∠PAB为钝角时点A的纵坐标y1的取值范围为(-∞,-1)∪(-1,-
).
提分百分百检测卷单元期末测试卷系列答案