Question

（05年天津卷）（14分）

抛物线C的方程为，过抛物线C上一点  ()作斜率为的两条直线分别交抛物线C于，两点（P、A、B三点互不相同），且满足（≠0且）。

（Ⅰ）求抛物线C的焦点坐标和准线方程

（Ⅱ）设直线AB上一点M，满足，证明线段PM的中点在y轴上

（Ⅲ）当时，若点P的坐标为（1，1），求∠PAB为钝角时点A的纵坐标的取值范围。

 

Answer 1

解析：（I）由抛物线的方程得，焦点坐标为（），准线方程为

（II）证明：设直线PA的方程为，直线PB的方程为

点和点的坐标是方程组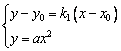的解

将代入得：

由韦达定理： ①

同理：，又因为，所以  ②

设点的坐标为，由，得  ③

将 ② 代入 ③ 得：

即：。所以，线段的中点在轴上

（III）因为点P（1，1）在抛物线上，所以，抛物线的方程为。

由 ① 得：，代入得

将代入 ② ，得，代入得

因此，直线PA、PB分别与抛物线C的交点A、B的坐标为

于是：，

因为为钝角且P、A、B三点互不相同，故必有，即

解得的范围为：或

又点A的纵坐标满足，故

当时，

当时，

所以，为钝角时，点A的纵坐标的取值范围是