（2011•莆田模拟）如图（1），在直角梯形ACC₁A₁中，∠CAA₁=90°，AA₁∥CC₁，AA₁=4，AC=3，CC₁=1，点B在线段AC上，AB=2BC，BB₁∥AA₁，且BB₁交A₁C₁于点B₁．现将梯形ACC₁A₁沿直线BB₁折成二面角A-BB₁-C，设其大小为θ．
（1）在上述折叠过程中，若90°≤θ≤180°，请你动手实验并直接写出直线A₁B₁与平面BCC₁B₁所成角的取值范围．（不必证明）；
（2）当θ=90°时，连接AC、A₁C₁、AC₁，得到如图（2）所示的几何体ABC-A₁B₁C₁，
（i）若M为线段AC₁的中点，求证：BM∥平面A₁B₁C₁；
（ii）记平面A₁B₁C₁与平面BCC₁B₁所成的二面角为α（0＜α≤90°），求cosa的值．

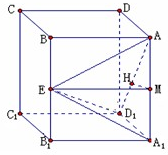正四棱柱ABCD-A₁B₁C₁D₁中，底面边长为a，侧棱AA₁长为ka（k＞0），E为侧棱BB₁的中点，记以AD₁为棱，EAD₁，A₁AD₁为面的二面角大小为θ．
（1）是否存在k值，使直线AE⊥平面A₁D₁E，若存在，求出k值；若不存在，说明理由；
（2）试比较tanθ与2

2

的大小．

二面角α-1-β内点P到两个面的距离分别为

2

，

3

，到棱的距离为2，则此二面角大小为．