摘要:在复习中主要熟练公式的各种变形.注意公式的逆向使用.变形使用.掌握恒等变形的基本方法:异角化同角.高次化低次.特殊值与特殊角的转换.条件的代入等.在做题过程中.要注意做到:过程详细.不能遗漏任何一个知识点.[知识回顾]
网址:http://m.1010jiajiao.com/timu_id_177628[举报]
在某测试中,卷面满分为100分,60分及以上为及格,为了调查午休对本次测试前两个月复习效果的影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如表所示:
参考公式及数据:K2=
(1)根据上述表格完成列联表:
(2)能否在犯错误的概率不超过0.025的前提下认为午休与考生及格有关系?对今后的复习有什么指导意义?
查看习题详情和答案>>
| 分数段 | [29~40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 午休考生 人数 |
23 | 47 | 30 | 21 | 14 | 31 | 14 |
| 不午休考 生人数 |
17 | 51 | 67 | 15 | 30 | 17 | 3 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| 及格人数 | 不及格人数 | 总计 | |
| 午休 | |||
| 不午休 | |||
| 总计 |
20.在二项式 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列
(1)求展开式的常数项; (2)求展开式中二项式系数最大的项;
(3)求展开式中各项的系数和。
【解析】本试题主要考查了二项式定理中通项公式和二项式系数的概念以及求解各个系数和的运用,赋值法思想要深刻体会。
查看习题详情和答案>>
(本题满分12分)已知函数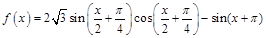 。
。
(1)求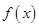 的最小正周期;
的最小正周期;
(2)若将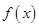 的图象向右平移
的图象向右平移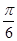 个单位,得到函数
个单位,得到函数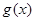 的图象,求函数
的图象,求函数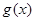 在区间
在区间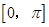 上的最大值和最小值。
上的最大值和最小值。
【解析】第一问中主要利用三角函数的两角和差公式化简为单一三角函数解析式
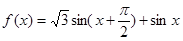 =
=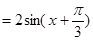
然后利用周期公式得到第一问。
第二问中,由于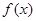 的图象向右平移
的图象向右平移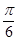 个单位,得到函数
个单位,得到函数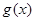 的图象,
的图象,
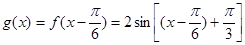
然后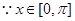 时,
时,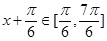 结合三角函数值域求解得到范围。
结合三角函数值域求解得到范围。
查看习题详情和答案>>
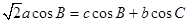 。
。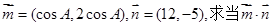 取最大值时,tanC的值。
取最大值时,tanC的值。