题目内容
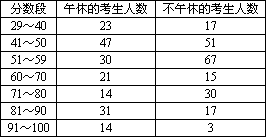
在某测试中,卷面满分为100分,60分及以上为及格,为了调查午休对本次测试前两个月复习效果的影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如表所示:
参考公式及数据:K2=
(1)根据上述表格完成列联表:
(2)能否在犯错误的概率不超过0.025的前提下认为午休与考生及格有关系?对今后的复习有什么指导意义?
| 分数段 | [29~40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 午休考生 人数 |
23 | 47 | 30 | 21 | 14 | 31 | 14 |
| 不午休考 生人数 |
17 | 51 | 67 | 15 | 30 | 17 | 3 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| 及格人数 | 不及格人数 | 总计 | |
| 午休 | |||
| 不午休 | |||
| 总计 |
分析:(1)根据题表中数据可以得到列联表;
(2)计算K2的值,与临界值比较,即可得出结论.
(2)计算K2的值,与临界值比较,即可得出结论.
解答:解:(1)根据题表中数据可以得到列联表如表:
(5分)
(2)据上表知:K2=
=
≈5.7
∵K2≈5.7>5.024,
因此,有97.5%的把握认为午休与考生及格有关系,即能在犯错误的概率不超过0.025的前提下认为午休与考生及格有关系.(10分)
对今后的复习的指导意义就是:在以后的复习中,考生应尽量适当午休,以保持最佳的学习状态.(11分)
| 及格人数 | 不及格人数 | 总计 | |
| 午休 | 80 | 100 | 180 |
| 不午休 | 65 | 135 | 200 |
| 总计 | 145 | 235 | 380 |
(2)据上表知:K2=
| 380(135×80-65×100)2 |
| 145×235×180×200 |
| 380×4300×4300 |
| 145×235×180×200 |
∵K2≈5.7>5.024,
因此,有97.5%的把握认为午休与考生及格有关系,即能在犯错误的概率不超过0.025的前提下认为午休与考生及格有关系.(10分)
对今后的复习的指导意义就是:在以后的复习中,考生应尽量适当午休,以保持最佳的学习状态.(11分)
点评:本题考查独立性检验知识的运用,考查学生的计算能力,正确计算K2的值,与临界值比较是关键.

练习册系列答案
相关题目
在某测试中,卷面满分为100分,60分为及格,为了调查午休对本次测试前两个月复习效果的影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如下表所示:
分数段 | 午休的考生成绩 | 不午休的考生成绩 |
29~40 | 23 | 17 |
41~50 | 47 | 51 |
51~59 | 30 | 67 |
60~70 | 21 | 15 |
71~80 | 14 | 30 |
81~90 | 31 | 17 |
91~100 | 14 | 3 |
(1)请根据上述表格完成列联表.
| 及格人数 | 不及格人数 | 总计 |
午休 |
|
|
|
不午休 |
|
|
|
总计 |
|
|
|
(2)根据列联表可以得出什么样的结论?对今后的复习有什么指导意义?
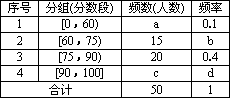
 11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.