网址：http://m.1010jiajiao.com/timu_id_176406[举报]
一、选择题(每小题5分，共50分)
1．C 2．B 3．D 4．A 5．C 6．B 7．A 8．C 9．B 10．D
二、填空题(每小题4分．共24分)
11．5
12．4 13．3825 14．
15．
16．3
三．解答题(本大题共6小题，共76分)
17．(本题12分)
解：(Ⅰ)∵
，
∴
………………………(2分)
∴
………………………(3分)
∴
……………………(4分)
∵在
中，
∴
………………………(5分)
(Ⅱ)设
分别是中
的对边，
∵?
∴
∴
① ……………………(6分)
由正弦定理：
，得 
……………………(7分)
∴
∴
② ……………………(8分)
由①②解得
……………………(9分)
由余弦定理，得
………………(10分)
………………(11分)
∴
，即边
的长为
。
……………………(12分)
18．(本题12分]
解：(Ⅰ)∵
是偶函数，
∴
，即
……(2分)
………………………………(4分)
∴
对一切
恒成立。
∴
……………………………………(6分)
(Ⅱ)由
………………(7分)
…………………(8分)
∵错误！不能通过编辑域代码创建对象。≥
……………………(10分)
∴
≥
…………………(11分)
∴
≤
∴若使方程
有解，则的取值范围是≤
………………(12分)
19．(本题12分)
解：(Ⅰ) ∵
分别是
的中点，
∴
且
……………………(1分)
∵
平面
,
平面
∴
平面
…………………………(2分)
∵
平面
平面
，
平面
∴
…………………………(4分)
∵
是
的中点，
∴
是
的中点．
∴
………………………(5分)
∴
∴四边形是平行四边形 …………………………(6 分)
(Ⅱ)当
时，平面
平面
…………………(8分)
在
上取一点，
连接
当
时，
∵
，
∴
即当时，
，
……………………(9分)
∵，，
∴
平面
……………………(10分)
∵
∴
平面
……………………………(11分)
∵平面
∴平面
平面
…………………………………(12分)
20．(本题12分)
解：(Ⅰ) ∵
∴
………………………………(2分)
∵在区间
上为减函数
∴
≤O在区间上恒成立 …………………………(3分)
∵是开口向上的抛物线
≤
≤
∴只需 即 …………………………(5分)
≤ 
≤
∴
≤
≤
………………………………………(6分)
(Ⅱ)当
时，
∴存在
，使得
∴在区间内有且只有一个极小值点 ……………(8分)
当
时
∴存在，使得
∴在区间内有且只有一个极大值点 ……………(10分)
当≤≤时，由(Ⅰ)可知在区间上为减函数
∴在区间内没有极值点．
综上可知，当时，
在区间内的极值点个数为
当≤≤时，在区间内的极值点个数为
………(12分)
21．(本题14分)
解：(Ⅰ)设椭圆的长半轴长为，短半轴长
，半焦距为
，
由离心率
，得
∵
∴
① …………………(2分)
∵直线的方程为
，原点
到直线的距离为
，
∴
② …………………(4分)
①代人②，解得
………………………(6分)
∴椭圆的标准方程为
…………………………(7分)
(Ⅱ) ∵
∴?=
∴?=?(-)=2 …………………(9分)
设
,则，即
………………(10分)
∴?=2
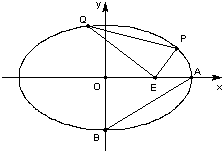已知中心在原点O，焦点在x轴上的椭圆C的离心率为
| ||
| 2 |
6
| ||
| 5 |
（1）求椭圆C的标准方程；
（2）已知点E（3，0），设点P、Q是椭圆C上的两个动点，满足EP⊥EQ，求
| EP |
| QP |
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点Q（-2，0）作直线l与椭圆C相交于A、B两点，直线m是过点(-
| 4 |
| 17 |
| a |
| ON |
| OA |
| OB |
| x2 |
| a2 |
| y2 |
| b2 |
（1）求椭圆的标准方程；
（2）已知Q（x0，y0）为椭圆上任意一点，求以Q为切点，椭圆的切线方程．
（3）设点P为直线x=4上一动点，过P作椭圆两条切线PA，PB，求证直线AB过定点，并求出该定点的坐标． 查看习题详情和答案>>