网址：http://m.1010jiajiao.com/timu_id_176379[举报]
一、选择题(每小题5分，共50分)
1．C 2．B 3．D 4．A 5．C 6．B 7．A 8．C 9．B 10．D
二、填空题(每小题4分．共24分)
11．5
12．4 13．3825 14．
15．
16．3
三．解答题(本大题共6小题，共76分)
17．(本题12分)
解：(Ⅰ)∵
，
∴
………………………(2分)
∴
………………………(3分)
∴
……………………(4分)
∵在
中，
∴
………………………(5分)
(Ⅱ)设
分别是中
的对边，
∵?
∴
∴
① ……………………(6分)
由正弦定理：
，得 
……………………(7分)
∴
∴
② ……………………(8分)
由①②解得
……………………(9分)
由余弦定理，得
………………(10分)
………………(11分)
∴
，即边
的长为
。
……………………(12分)
18．(本题12分]
解：(Ⅰ)∵
是偶函数，
∴
，即
……(2分)
………………………………(4分)
∴
对一切
恒成立。
∴
……………………………………(6分)
(Ⅱ)由
………………(7分)
…………………(8分)
∵错误！不能通过编辑域代码创建对象。≥
……………………(10分)
∴
≥
…………………(11分)
∴
≤
∴若使方程
有解，则的取值范围是≤
………………(12分)
19．(本题12分)
解：(Ⅰ) ∵
分别是
的中点，
∴
且
……………………(1分)
∵
平面
,
平面
∴
平面
…………………………(2分)
∵
平面
平面
，
平面
∴
…………………………(4分)
∵
是
的中点，
∴
是
的中点．
∴
………………………(5分)
∴
∴四边形是平行四边形 …………………………(6 分)
(Ⅱ)当
时，平面
平面
…………………(8分)
在
上取一点，
连接
当
时，
∵
，
∴
即当时，
，
……………………(9分)
∵，，
∴
平面
……………………(10分)
∵
∴
平面
……………………………(11分)
∵平面
∴平面
平面
…………………………………(12分)
20．(本题12分)
解：(Ⅰ) ∵
∴
………………………………(2分)
∵在区间
上为减函数
∴
≤O在区间上恒成立 …………………………(3分)
∵是开口向上的抛物线
≤
≤
∴只需 即 …………………………(5分)
≤ 
≤
∴
≤
≤
………………………………………(6分)
(Ⅱ)当
时，
∴存在
，使得
∴在区间内有且只有一个极小值点 ……………(8分)
当
时
∴存在，使得
∴在区间内有且只有一个极大值点 ……………(10分)
当≤≤时，由(Ⅰ)可知在区间上为减函数
∴在区间内没有极值点．
综上可知，当时，
在区间内的极值点个数为
当≤≤时，在区间内的极值点个数为
………(12分)
21．(本题14分)
解：(Ⅰ)设椭圆的长半轴长为，短半轴长
，半焦距为
，
由离心率
，得
∵
∴
① …………………(2分)
∵直线的方程为
，原点
到直线的距离为
，
∴
② …………………(4分)
①代人②，解得
………………………(6分)
∴椭圆的标准方程为
…………………………(7分)
(Ⅱ) ∵
∴?=
∴?=?(-)=2 …………………(9分)
设
,则，即
………………(10分)
∴?=2
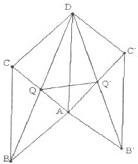如图，矩形ABCD与矩形AB′C′D全等，且所在平面所成的二面角为a，记两个矩形对角线的交点分别为Q，Q′，AB=a，AD=b．（1）求证：QQ′∥平面ABB′；
（2）当b=
| 2 |
| π |
| 3 |
（3）当a＞b，且AC⊥DB'时，求二面角a的余弦值（用a，b表示）． 查看习题详情和答案>>
某先生居住在城镇的A处，准备开车到单位B处上班，若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率，如图．（ 例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为| 1 |
| 10 |
| 1 |
| 15 |
（1）请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小；
（2）若记ξ路线A→（3）C→（4）F→（5）B中遇到堵车次数为随机变量ξ，求ξ的数学期望Eξ．
甲校：
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 3 | 4 | 8 | 15 |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
（Ⅲ）由以上统计数据填写右面2×2列联表，并判断是否有90%的把握认为两个学校的数学成绩有差异．
参考数据与公式：
由列联表中数据计算K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表
| P（K≥k0） | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
计算机中常用16进制，采用数字0～9和字母A～F共16个计数符号与10进制得对应关系如下表：
|