题目内容
已知函数f(x)=log2(2x+1).
(1)求证:函数f(x)定义域内单调递增;
(2)记g(x)=log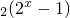 .若关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.
.若关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.
(1)证明:任取x1<x2,则f(x1)-f(x2)=log2(2x1+1)-log2(2x2+1)=log2
∵x1<x2,∴0< <1,∴log2
<1,∴log2 <0
<0
∴f(x1)<f(x2)
∴函数f(x)在R上单调递增;
(2)解:∵g(x)=log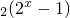 ,x>0,
,x>0,
∴m=g(x)-f(x)=log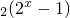 -log2(2x+1)=log2(1-
-log2(2x+1)=log2(1- ).
).
当1≤x≤2时,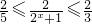 ,
,
∴ ≤1-
≤1- ≤
≤
∴m的取值范围是 .
.
分析:(1)利用函数单调性的定义,证明函数f(x)在R上单调递增,步骤为取值、作差、变形定号、下结论;
(2)关于x的方程g(x)=m+f(x)在[1,2]上有解,转化为求m=g(x)-f(x)在[1,2]上的值域问题.
点评:本题考查函数单调性的证明,考查学生转化问题的能力,考查求函数的值域,属于中档题.

∵x1<x2,∴0<
 <1,∴log2
<1,∴log2 <0
<0∴f(x1)<f(x2)
∴函数f(x)在R上单调递增;
(2)解:∵g(x)=log
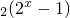 ,x>0,
,x>0,∴m=g(x)-f(x)=log
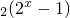 -log2(2x+1)=log2(1-
-log2(2x+1)=log2(1- ).
).当1≤x≤2时,
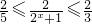 ,
,∴
 ≤1-
≤1- ≤
≤
∴m的取值范围是
 .
.分析:(1)利用函数单调性的定义,证明函数f(x)在R上单调递增,步骤为取值、作差、变形定号、下结论;
(2)关于x的方程g(x)=m+f(x)在[1,2]上有解,转化为求m=g(x)-f(x)在[1,2]上的值域问题.
点评:本题考查函数单调性的证明,考查学生转化问题的能力,考查求函数的值域,属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目