摘要:设{Sn}是第n个正方形的面积,则Sn是以为首项, 为公比的等比数列. 4分
网址:http://m.1010jiajiao.com/timu_id_15819[举报]
(2013•汕尾二模)设等比数列{an}的前n项和为Sn,已知an+1=2Sn+2(n∈N*).
(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成公差为dn的等差数列(如:在a1与a2之间插入1个数构成第一个等差数列,其公差为d1;在a2与a3之间插入2个数构成第二个等差数列,其公差为d2,…以此类推),设第n个等差数列的和是An.是否存在一个关于n的多项式g(n),使得An=g(n)dn对任意n∈N*恒成立?若存在,求出这个多项式;若不存在,请说明理由;
(3)对于(2)中的数列d1,d2,d3,…,dn,…,这个数列中是否存在不同的三项dm,dk,dp(其中正整数m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由.
查看习题详情和答案>>
(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成公差为dn的等差数列(如:在a1与a2之间插入1个数构成第一个等差数列,其公差为d1;在a2与a3之间插入2个数构成第二个等差数列,其公差为d2,…以此类推),设第n个等差数列的和是An.是否存在一个关于n的多项式g(n),使得An=g(n)dn对任意n∈N*恒成立?若存在,求出这个多项式;若不存在,请说明理由;
(3)对于(2)中的数列d1,d2,d3,…,dn,…,这个数列中是否存在不同的三项dm,dk,dp(其中正整数m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由.
已知数集序列{1},{3,5},{7,9,11},{13,15,17,19},…,其中第n个集合有n个元素,每一个集合都由连续正奇数组成,并且每一个集合中的最大数与后一个集合中的最小数是连续奇数.
(1)求第n个集合中各数之和Sn的表达式;
(2)设n是不小于2的正整数,f(n)=
,求证:n+
f(i)=nf(n).
查看习题详情和答案>>
(1)求第n个集合中各数之和Sn的表达式;
(2)设n是不小于2的正整数,f(n)=
| n |
 |
| i=1 |
| 1 | |||
|
| n-1 |
 |
| i=1 |
已知点P1(a1,b1),P2(a2,b2),…,Pn(an,bn)(n为正整数)都在函数y=(
)x的图象上.
(1)若数列{an}是首项为1,公差也为1的等差数列,求{bn}的通项公式;
(2)对(1)中的数列{an}和{bn},过点Pn,Pn+1的直线与两坐标轴所围成的三角形面积为cn,试证明:对一切正整数n,cn≤
;
(3)对(1)中的数列{an},对每个正整数k,在ak与ak+1之间插入3k-1个3,得到一个新的数列{dn},问a5是数列{dn}中的第几项.若设Sn是数列{dn}的前n项和,试求S100的值. 查看习题详情和答案>>
| 1 |
| 2 |
(1)若数列{an}是首项为1,公差也为1的等差数列,求{bn}的通项公式;
(2)对(1)中的数列{an}和{bn},过点Pn,Pn+1的直线与两坐标轴所围成的三角形面积为cn,试证明:对一切正整数n,cn≤
| 9 |
| 8 |
(3)对(1)中的数列{an},对每个正整数k,在ak与ak+1之间插入3k-1个3,得到一个新的数列{dn},问a5是数列{dn}中的第几项.若设Sn是数列{dn}的前n项和,试求S100的值. 查看习题详情和答案>>
已知点P1(a1,b1),P2(a2,b2),…,Pn(an,bn)(n为正整数)都在函数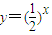 的图象上.
的图象上.
(1)若数列{an}是首项为1,公差也为1的等差数列,求{bn}的通项公式;
(2)对(1)中的数列{an}和{bn},过点Pn,Pn+1的直线与两坐标轴所围成的三角形面积为cn,试证明:对一切正整数n,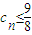 ;
;
(3)对(1)中的数列{an},对每个正整数k,在ak与ak+1之间插入3k-1个3,得到一个新的数列{dn},问a5是数列{dn}中的第几项.若设Sn是数列{dn}的前n项和,试求S100的值.
查看习题详情和答案>>
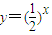 的图象上.
的图象上.(1)若数列{an}是首项为1,公差也为1的等差数列,求{bn}的通项公式;
(2)对(1)中的数列{an}和{bn},过点Pn,Pn+1的直线与两坐标轴所围成的三角形面积为cn,试证明:对一切正整数n,
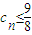 ;
;(3)对(1)中的数列{an},对每个正整数k,在ak与ak+1之间插入3k-1个3,得到一个新的数列{dn},问a5是数列{dn}中的第几项.若设Sn是数列{dn}的前n项和,试求S100的值.
查看习题详情和答案>>
设等比数列{an}的前n项和为Sn,已知 .
.
(1)求数列{an}的通项公式;
(2)在an与a n+1之间插入n个数,使这n+2个数组成公差为dn的等差数列(如:在a1与a2之间插入1个数构成第一个等差数列,其公差为d1;在a2与a3之间插入2个数构成第二个等差数列,其公差为d2,…以此类推),设第n个等差数列的和是An.是否存在一个关于n的多项式g(n),使得An=g(n)dn对任意n∈N*恒成立?若存在,求出这个多项式;若不存在,请说明理由;
(3)对于(2)中的数列d1,d2,d3,…,dn,…,这个数列中是否存在不同的三项dm,dk,dp(其中正整数m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由.
查看习题详情和答案>>
 .
.(1)求数列{an}的通项公式;
(2)在an与a n+1之间插入n个数,使这n+2个数组成公差为dn的等差数列(如:在a1与a2之间插入1个数构成第一个等差数列,其公差为d1;在a2与a3之间插入2个数构成第二个等差数列,其公差为d2,…以此类推),设第n个等差数列的和是An.是否存在一个关于n的多项式g(n),使得An=g(n)dn对任意n∈N*恒成立?若存在,求出这个多项式;若不存在,请说明理由;
(3)对于(2)中的数列d1,d2,d3,…,dn,…,这个数列中是否存在不同的三项dm,dk,dp(其中正整数m,k,p成等差数列)成等比数列,若存在,求出这样的三项;若不存在,说明理由.