题目内容
已知数集序列{1},{3,5},{7,9,11},{13,15,17,19},…,其中第n个集合有n个元素,每一个集合都由连续正奇数组成,并且每一个集合中的最大数与后一个集合中的最小数是连续奇数.
(1)求第n个集合中各数之和Sn的表达式;
(2)设n是不小于2的正整数,f(n)=
,求证:n+
f(i)=nf(n).
(1)求第n个集合中各数之和Sn的表达式;
(2)设n是不小于2的正整数,f(n)=
| n |
 |
| i=1 |
| 1 | |||
|
| n-1 |
 |
| i=1 |
分析:(1)第一个集合中有一个数,第二个集合中有2个数,第三个集合中有3个数,…第n个集合中有n个数,利用等差数列求和公式计算an前共有多少个奇数,从而得到第n个集合中各数之和Sn的表达式.
(2)由(1)得f(n)=
=1+
+
+…+
.用数学归纳法证明整除问题时分为两个步骤,第一步,先证明当当n=1时,结论显然成立,第二步,先假设假设当n=k时结论成立,利用此假设结合因式的配凑法,证明当n=k+1时,结论也成立即可.
(2)由(1)得f(n)=
| n |
 |
| i=1 |
| 1 | |||
|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
解答:解:(1)设第n个集合中的最小数为an,则an前共有1+2+3+…+(n-1)=
个奇数,
∴an=2×[
+1]-1=n2-n+1. …(3分)
从而Sn=n(n2-n+1)+
×2=n3. …(5分)
(2)由(1)得,
=i(i=1,2,3,…,n),
∴f(n)=
=1+
+
+…+
.
下面用数学归纳法证明n+
f(i)=nf(n). …(7分)
当n=2时,左边=2+f(1)=3,右边=2f(2)=2(1+
)=3,等式成立;
假设n=k(k≥2)时,等式成立,即k+f(1)+f(2)+…+f(k-1)=kf(k)成立,
那么,当n=k+1时,
左边=(k+1)+f(1)+f(2)+…+f(k-1)+f(k)=kf(k)+1+f(k)=(k+1)f(k)+1=(k+1)
+1.
右边=(k+1)f(k+1)=(k+1)
=(k+1)[
+
]=(k+1)
+1,
即左边=右边,
∴等式也成立.…(9分)
综上可知,对一切不小于2的正整数n,等式n+
f(i)=nf(n)都成立.…(10分)
| n(n-1) |
| 2 |
∴an=2×[
| n(n-1) |
| 2 |
从而Sn=n(n2-n+1)+
| n(n-1) |
| 2 |
(2)由(1)得,
| 3 | Si |
∴f(n)=
| n |
 |
| i=1 |
| 1 | |||
|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
下面用数学归纳法证明n+
| n-1 |
 |
| i=1 |
当n=2时,左边=2+f(1)=3,右边=2f(2)=2(1+
| 1 |
| 2 |
假设n=k(k≥2)时,等式成立,即k+f(1)+f(2)+…+f(k-1)=kf(k)成立,
那么,当n=k+1时,
左边=(k+1)+f(1)+f(2)+…+f(k-1)+f(k)=kf(k)+1+f(k)=(k+1)f(k)+1=(k+1)
| k |
 |
| i=1 |
| 1 |
| i |
右边=(k+1)f(k+1)=(k+1)
| k+1 |
 |
| i=1 |
| 1 |
| i |
| k |
 |
| i=1 |
| 1 |
| i |
| 1 |
| k+1 |
| k |
 |
| i=1 |
| 1 |
| i |
即左边=右边,
∴等式也成立.…(9分)
综上可知,对一切不小于2的正整数n,等式n+
| n-1 |
 |
| i=1 |
点评:本题考查数列求和的方法,注意集合中元素的特征及元素个数的规律;本题还考查数学归纳法,数学归纳法的基本形式:
设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基)2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.
设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基)2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
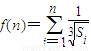 ,求证:
,求证: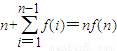 .
.