摘要：而是一类裂项后有明显相消项的数列,所以采用了裂项法.但相消时应注意消去项的规律,即消去了哪些项,保留了哪些项.
网址：http://m.1010jiajiao.com/timu_id_15811[举报]
已知0≤a＜2，0≤b＜4，为估计在a＞1的条件下，函数f（x）=x2+2ax+b有两相异零点的概率P．用计算机产生了[{0，1}）内的两组随机数a1，b1各2400个，并组成了2400个有序数对（a1，b1），统计这2400个有序数对后得到2×2列联表的部分数据如下表：
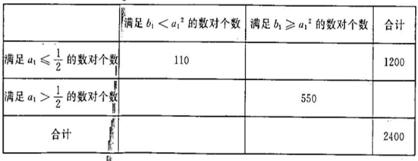
则数据表中数据计算出的概率P的估计值为（ ）
则数据表中数据计算出的概率P的估计值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知有穷数列A：a1，a2，…，an，（n≥2）．若数列A中各项都是集合{x|-1＜x＜1}的元素，则称该数列为
数列．对于数列A，定义如下操作过程T：从A中任取两项ai，aj，将
的值添在A的最后，然后删除ai，aj，这样得到一个n-1项的新数列A1（约定：一个数也视作数列）．若A1还是数列，可继续实施操作过程T，得到的新数列记作A2，…，如此经过k次操作后得到的新数列记作Ak．
（Ⅰ）设A：0，
，
…请写出A1的所有可能的结果；
（Ⅱ）求证：对于一个n项的数列A操作T总可以进行n-1次；
（Ⅲ）设A：-
，-
，-
，-
，
，
，
，
，
，
…求A9的可能结果，并说明理由．
查看习题详情和答案>>
数列．对于数列A，定义如下操作过程T：从A中任取两项ai，aj，将| ai+aj |
| 1+aiaj |
数列，可继续实施操作过程T，得到的新数列记作A2，…，如此经过k次操作后得到的新数列记作Ak．（Ⅰ）设A：0，
| 1 |
| 2 |
| 1 |
| 3 |
（Ⅱ）求证：对于一个n项的
数列A操作T总可以进行n-1次；（Ⅲ）设A：-
| 5 |
| 7 |
| 1 |
| 6 |
| 1 |
| 5 |
| 1 |
| 4 |
| 5 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
已知有穷数列A：a1，a2，…，an，（n≥2）．若数列A中各项都是集合{x|-1＜x＜1}的元素，则称该数列为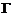
数列．对于
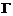数列A，定义如下操作过程T：从A中任取两项ai，aj，将
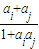的值添在A的最后，然后删除ai，aj，这样得到一个n-1项的新数列A1（约定：一个数也视作数列）．若A1还是
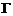数列，可继续实施操作过程T，得到的新数列记作A2，…，如此经过k次操作后得到的新数列记作Ak．
（Ⅰ）设A：0，
，
…请写出A1的所有可能的结果；
（Ⅱ）求证：对于一个n项的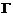
数列A操作T总可以进行n-1次；
（Ⅲ）设A：-
，-
，-
，-
，
，
，
，
，
，
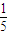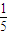…求A9的可能结果，并说明理由．
查看习题详情和答案>>
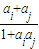的值添在A的最后，然后删除ai，aj，这样得到一个n-1项的新数列A1（约定：一个数也视作数列）．若A1还是（Ⅰ）设A：0，
，…请写出A1的所有可能的结果；（Ⅱ）求证：对于一个n项的
（Ⅲ）设A：-
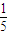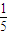，-，-，-，，，，，，…求A9的可能结果，并说明理由．查看习题详情和答案>>
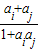的值添在A的最后，然后删除ai，aj，这样得到一个n-1项的新数列A1（约定：一个数也视作数列）．若A1还是
，
…请写出A1的所有可能的结果；
，-
，-
，-
，
，
，
，
，
，
…求A9的可能结果，并说明理由．