��Ŀ����
��֪��������A��a1��a2������an����n��2����������A�и���Ǽ���{x|-1��x��1}��Ԫ�أ���Ƹ�����Ϊ ���У�����
���У����� ����A���������²�������T����A����ȡ����ai��aj����
����A���������²�������T����A����ȡ����ai��aj����
��ֵ����A�����Ȼ��ɾ��ai��aj�������õ�һ��n-1���������A1��Լ����һ����Ҳ�������У�����A1���� ���У��ɼ���ʵʩ��������T���õ��������м���A2��������˾���k�β�����õ��������м���Ak��
���У��ɼ���ʵʩ��������T���õ��������м���A2��������˾���k�β�����õ��������м���Ak��
������A��0��
��
����д��A1�����п��ܵĽ����
������֤������һ��n��� ����A����T�ܿ��Խ���n-1�Σ�
����A����T�ܿ��Խ���n-1�Σ�
������A��-
��-
��-
��-
��
��
��
��
��
��
����A9�Ŀ��ܽ������˵�����ɣ�
 ��������
���У����� ����A���������²�������T����A����ȡ����ai��aj����
����A���������²�������T����A����ȡ����ai��aj����| ai+aj |
| 1+aiaj |
 ���У��ɼ���ʵʩ��������T���õ��������м���A2��������˾���k�β�����õ��������м���Ak��
���У��ɼ���ʵʩ��������T���õ��������м���A2��������˾���k�β�����õ��������м���Ak��������A��0��
| 1 |
| 2 |
| 1 |
| 3 |
������֤������һ��n���
 ����A����T�ܿ��Խ���n-1�Σ�
����A����T�ܿ��Խ���n-1�Σ�������A��-
| 5 |
| 7 |
| 1 |
| 6 |
| 1 |
| 5 |
| 1 |
| 4 |
| 5 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
����������ֱ�Ӱ�������������ÿ��ȡ������������㼴�����A1�����п��ܵĽ����
������ͨ������õ�ÿ�β���������������T���У��ٸ���ÿ�β����ж�������һ�ɾ������ɵõ����ۣ�
�����ȶ������㣺a��b=
����֤�������������㽻���ɺͽ���ɣ��ٽ�ϣ���֪A9�н���һ��ٰ����������A5���ۺϼ��ɵõ�A9�Ŀ��ܽ����
������ͨ������õ�ÿ�β���������������T���У��ٸ���ÿ�β����ж�������һ�ɾ������ɵõ����ۣ�
�����ȶ������㣺a��b=
| a+b |
| 1+ab |
����⣺����ֱ�Ӱ���������������ȡ0��
ʱ�������ɵã�A1��
��
��
��ȡ0��
ʱ�ɵ�A1��
��
��
��ȡ
��
ʱ���ɵ�A1��0��
��
�������µ����ֿ��ܽ����A1��
��
��A1��
��
��A1��0��
������3�֣�
��������?a��b��{x|-1��x��1}����
-1=
��0��
-(-1)=
��0
����
��{x|-1��x��1}��
��ÿ�β���������������T���У�
������ÿ�β����ж�������һ�ɾ�����
���Զ�T����Aÿ����һ�Σ������ͼ���һ�
���Զ�n���T����A�ɽ��У�n-1���β��������ֻʣ��һ�����7�֣�
�����ɣ���֪A9�н���һ�
��������a��b��{x|-1��x��1}��ʵ��a��b�������㣺a��b=
��
����֤�������������㽻���ɺͽ���ɣ�
��Ϊa��b=
����b��a=
������a��b=b��a�������������㽻���ɣ�
��Ϊa�ѣ�b��c��=a��
=
=
�ң�a��b����c=
c=
=
����a�ѣ�b��c��=��a��b����c�����������������ɣ�
����A9�е�����ʵʩ�ľ������������ ����������12�֣�
ѡ�����²���������A9��
�ɣ���֪
��
=
��
��֪-
��
=0��-
��
=0��-
��
=0��-
��
=0��
����A5��
��0��0��0��0����
��֪A5����4�β�����ʣ��һ��Ϊ
��
���Ͽ�֪��A9��
������14�֣�
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
��ȡ0��
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
��ȡ
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 7 |
�������µ����ֿ��ܽ����A1��
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 7 |
��������?a��b��{x|-1��x��1}����
| a+b |
| 1+ab |
| -(a-1)(b-1) |
| 1+ab |
| a+b |
| 1+ab |
| (a+1)(b+1) |
| 1+ab |
����
| a+b |
| 1+ab |
��ÿ�β���������������T���У�
������ÿ�β����ж�������һ�ɾ�����
���Զ�T����Aÿ����һ�Σ������ͼ���һ�
���Զ�n���T����A�ɽ��У�n-1���β��������ֻʣ��һ�����7�֣�
�����ɣ���֪A9�н���һ�
��������a��b��{x|-1��x��1}��ʵ��a��b�������㣺a��b=
| a+b |
| 1+ab |
����֤�������������㽻���ɺͽ���ɣ�
��Ϊa��b=
| a+b |
| 1+ab |
| b+a |
| 1+ba |
��Ϊa�ѣ�b��c��=a��
| b+c |
| 1+bc |
a+
| ||
1+a•
|
| a+b+c+abc |
| 1+ab+bc+ac |
�ң�a��b����c=
| a+b |
| 1+ab |
| ||
1+
|
| a+b+c+abc |
| 1+ab+ac+bc |
����a�ѣ�b��c��=��a��b����c�����������������ɣ�
����A9�е�����ʵʩ�ľ������������ ����������12�֣�
ѡ�����²���������A9��
�ɣ���֪
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 7 |
��֪-
| 5 |
| 7 |
| 5 |
| 7 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 6 |
����A5��
| 5 |
| 6 |
��֪A5����4�β�����ʣ��һ��Ϊ
| 5 |
| 6 |
���Ͽ�֪��A9��
| 5 |
| 6 |
������������һ���ۺ��Ժ�ǿ���⣬����ʱҪ�������⣬���ⶨ�壬�������¶��������⣬��ϸ��𣬱������

��ϰ��ϵ�д�
�����Ŀ
 ��ֵ����A�����Ȼ��ɾ��ai��aj�������õ�һ��n-1���������A1(Լ����һ����Ҳ��������)����A1���Ǧ����У��ɼ���ʵʩ��������T���õ��������м���A2��������˾���k�β�����õ��������м���Ak��
��ֵ����A�����Ȼ��ɾ��ai��aj�������õ�һ��n-1���������A1(Լ����һ����Ҳ��������)����A1���Ǧ����У��ɼ���ʵʩ��������T���õ��������м���A2��������˾���k�β�����õ��������м���Ak�� ����д��A1�����п��ܵĽ����
����д��A1�����п��ܵĽ���� ����A9�Ŀ��ܽ������˵������.
����A9�Ŀ��ܽ������˵������. 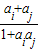 ��ֵ����A�����Ȼ��ɾ��ai��aj�������õ�һ��n-1���������A1��Լ����һ����Ҳ�������У�����A1����
��ֵ����A�����Ȼ��ɾ��ai��aj�������õ�һ��n-1���������A1��Լ����һ����Ҳ�������У�����A1���� ��
�� ����д��A1�����п��ܵĽ����
����д��A1�����п��ܵĽ���� ��-
��- ��-
��- ��-
��- ��
�� ��
�� ��
�� ��
�� ��
�� ��
�� ����A9�Ŀ��ܽ������˵�����ɣ�
����A9�Ŀ��ܽ������˵�����ɣ�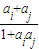 ��ֵ����A�����Ȼ��ɾ��ai��aj�������õ�һϵ��n-1���������A1 ��Լ����һ����Ҳ�������У�����A1�����п��ܽ���ظ���������T�ֵõ�һϵ��n-2���������A2����˾���k�β�����õ��������м���Ak����A��
��ֵ����A�����Ȼ��ɾ��ai��aj�������õ�һϵ��n-1���������A1 ��Լ����һ����Ҳ�������У�����A1�����п��ܽ���ظ���������T�ֵõ�һϵ��n-2���������A2����˾���k�β�����õ��������м���Ak����A�� ����A3�Ŀ��ܽ���ǣ� ��
����A3�Ŀ��ܽ���ǣ� ��

