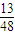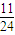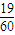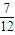题目内容
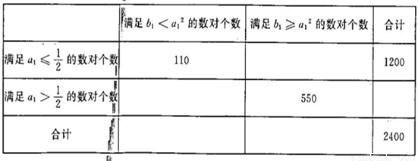
已知0≤a<2,0≤b<4,为估计在a>1的条件下,函数f(x)=x2+2ax+b有两相异零点的概率P.用计算机产生了[{0,1})内的两组随机数a1,b1各2400个,并组成了2400个有序数对(a1,b1),统计这2400个有序数对后得到2×2列联表的部分数据如下表:
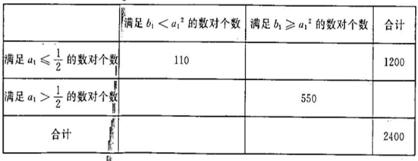
则数据表中数据计算出的概率P的估计值为( )

则数据表中数据计算出的概率P的估计值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:先求出使得函数f(x)=x2+2ax+b有两相异零点时a,b要满足的条件,即a2>b,从列联表中可以看出使得函数有两个相异的零点的数对数,条件中所给的共有2400对有序数对,求出概率.
解答:解:要使得函数f(x)=x2+2ax+b有两相异零点,
4a2-4b>0,
∴a2>b,
条件中所给的共有2400对有序数对,
在这些有序数对中,使得函数有两个相异的零点,
共有110+(1200-550)=760,
∴数据表中数据计算出的概率P的估计值是
=
.
故选C
4a2-4b>0,
∴a2>b,
条件中所给的共有2400对有序数对,
在这些有序数对中,使得函数有两个相异的零点,
共有110+(1200-550)=760,
∴数据表中数据计算出的概率P的估计值是
| 760 |
| 2400 |
| 19 |
| 60 |
故选C
点评:本题考查随机抽样和样本估计总体的实际应用,考查看出列联表中所给的数据,考查用概率统计知识解决实际问题,本题是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目