网址:http://m.1010jiajiao.com/timu_id_154257[举报]
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
A
B
B
C
C
D
D
D
A
A
二、填空题(每小题5分,共20分)
13. 14.
14.
 15. 1 16.
15. 1 16.

三、简答题
17.解:依题记“甲答对一题”为事件A ;“乙答对一题”为事件B
2分
则



∴ξ的分布列:
ξ
0
1
2
P



8分
∴ 10分
10分
18.解:当 时,原式
时,原式 3分
3分
当 时,有
时,有
∴原式= 7分
7分
当 时,
时,
∴原式 11分
11分
综上所述: 12分
12分
19.解:设切点( ),
), 3分
3分
∵切线与直线 平行
平行
∴

 或
或 10分
10分
∴切点坐标(1,-8)(-1,-12)
∴切线方程: 或
或
即: 或
或 12分
12分

21.解:设底面一边长为 ,则另一边长
,则另一边长
∴高为 3分
3分
由:
 ∴
∴
∵体积
 6分
6分
令 得
得 或
或 (舍去)
(舍去)
∵ 只有一个极值点
只有一个极值点
∴ ,此时高
,此时高 11分
11分
答:高为 12分
12分
22.解:假设 存在
存在
当 时,由
时,由 即:
即:
∴
当 时,
时, ∴
∴
猜想:
证明:1. 当 时,已证
时,已证
2. 假设 时结论成立
时结论成立

即为 时结论也成立
时结论也成立
由(1)(2)可知,对大于1的自然数n,存在 ,使
,使 成立 12分
成立 12分
(本小题满分12分)设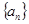 是单调递增的等差数列,
是单调递增的等差数列,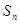 为其前n项和,且满足
为其前n项和,且满足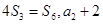 是
是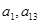 的等比中项.
的等比中项.
(I)求数列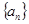 的通项公式;
的通项公式;
(II)是否存在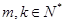 ,使
,使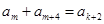 ?说明理由;
?说明理由;
(III)若数列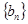 满足
满足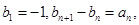 求数列
求数列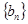 的通项公式.
的通项公式.
查看习题详情和答案>>
(本小题满分12分)设数列![]() 的通项公式为
的通项公式为![]() . 数列
. 数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值.(1)若
成立的所有n中的最小值.(1)若![]() ,求
,求![]() ;(2)若
;(2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
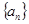 是单调递增的等差数列,
是单调递增的等差数列,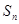 为其前n项和,且满足
为其前n项和,且满足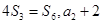 是
是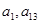 的等比中项.
的等比中项.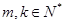 ,使
,使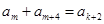 ?说明理由;
?说明理由;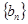 满足
满足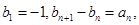 求数列
求数列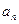 }的前n项和为
}的前n项和为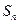 ,且
,且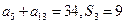 。
。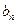 }的通项公式为
}的通项公式为 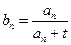 ,是否存在正整数t,使得
,是否存在正整数t,使得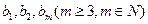 成等差数列?若存在,求出t和m的值;若不存在,请说明理由
成等差数列?若存在,求出t和m的值;若不存在,请说明理由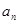 }的前n项和为
}的前n项和为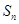 ,且
,且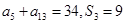 。
。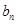 }的通项公式为
}的通项公式为
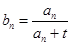 ,是否存在正整数t,使得
,是否存在正整数t,使得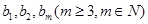 成等差数列?若存在,求出t和m的值;若不存在,请说明理由
成等差数列?若存在,求出t和m的值;若不存在,请说明理由