摘要：∴S1+S2+-+Sn==8［1-()n］;
网址：http://m.1010jiajiao.com/timu_id_15310[举报]
已知点P是直角坐标平面内的动点，点P到直线l1：x=-2的距离为d1，到点F（-1，0）的距离为d2，且
=
．
（1）求动点P所在曲线C的方程；
（2）直线l过点F且与曲线C交于不同两点A、B（点A或B不在x轴上），分别过A、B点作直线l1：x=-2的垂线，对应的垂足分别为M、N，试判断点F与以线段MN为直径的圆的位置关系（指在圆内、圆上、圆外等情况）；
（3）记S1=S△FAM，S2=S△FMN，S3=S△FBN（A、B、M、N是（2）中的点），问是否存在实数λ，使S22=λS1S3成立．若存在，求出λ的值；若不存在，请说明理由．
进一步思考问题：若上述问题中直线l1：x=-
、点F（-c，0）、曲线C：
+
=1(a＞b＞0，c=
)，则使等式S22=λS1S3成立的λ的值仍保持不变．请给出你的判断 （填写“不正确”或“正确”）（限于时间，这里不需要举反例，或证明）．
查看习题详情和答案>>
| d2 |
| d1 |
| ||
| 2 |
（1）求动点P所在曲线C的方程；
（2）直线l过点F且与曲线C交于不同两点A、B（点A或B不在x轴上），分别过A、B点作直线l1：x=-2的垂线，对应的垂足分别为M、N，试判断点F与以线段MN为直径的圆的位置关系（指在圆内、圆上、圆外等情况）；
（3）记S1=S△FAM，S2=S△FMN，S3=S△FBN（A、B、M、N是（2）中的点），问是否存在实数λ，使S22=λS1S3成立．若存在，求出λ的值；若不存在，请说明理由．
进一步思考问题：若上述问题中直线l1：x=-
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
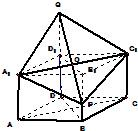如图，已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形，Q是侧棱DD1（DD1＞
| ||
| 2 |
（Ⅰ）证明：AC⊥QP；
（Ⅱ）当S取得最小值时，求cos∠A1QC1的值． 查看习题详情和答案>>
在△ABC中，若它的内切圆半径为r，周长为C，则它的面积S△ABC=
．请写出在正四面体中类似的命题：
查看习题详情和答案>>
| rC |
| 2 |
若四面体四个面的面积分别为S1，S2，S3，S4，内切球的半径为R，则此四面体的体积为：V=
（S1+S2+S3+S4）R
| 1 |
| 3 |
若四面体四个面的面积分别为S1，S2，S3，S4，内切球的半径为R，则此四面体的体积为：V=
（S1+S2+S3+S4）R
．| 1 |
| 3 |