题目内容
在△ABC中,若它的内切圆半径为r,周长为C,则它的面积S△ABC=
.请写出在正四面体中类似的命题:
| rC |
| 2 |
若四面体四个面的面积分别为S1,S2,S3,S4,内切球的半径为R,则此四面体的体积为:V=
(S1+S2+S3+S4)R
| 1 |
| 3 |
若四面体四个面的面积分别为S1,S2,S3,S4,内切球的半径为R,则此四面体的体积为:V=
(S1+S2+S3+S4)R
.| 1 |
| 3 |
分析:先用面积分割法,证明平面内的结论正确.然后将该命题推广到空间:若四面体四个面的面积分别为S1,S2,S3,S4,内切球的半径为R,则此四面体的体积为:V=
(S1+S2+S3+S4)R.接下来可以用体积分割的方法,类似地证明推广到空间中.
| 1 |
| 3 |
解答:解:若四面体四个面的面积分别为S1,S2,S3,S4,内切球的半径为R,则此四面体的体积为V=
(S1+S2+S3+S4)R.
证明如下:
设四面体ABCD的内切球为球O,球O分别切面BCD、面ACD、面ABD、面ABC于E、F、G、H,
分别设S△BCD、S△ACD、S△ABD、S△ABC为S1、S2、S3、S4
∵球O切平面BCD于点E,
∴OE⊥平面BCD,三棱锥O-BCD的体积为V1=
S△BCD•OE=
S1R,
同理可得:三棱锥O-BCD的体积为V2=
S△ACD•OF=
S2R,三棱锥O-ABD的体积为V3=
S△ABD•OG=
S3R,
三棱锥O-ABC的体积为V4=
S△ABC•OH=
S4R
∴四面体ABCD的体积等于V=V1+V2+V3+V4=
S1R+
S2R+
S3R+
S4R=
(S1+S2+S3+S4)R.
故答案为:四面体体积为V=
(S1+S2+S3+S4)R
| 1 |
| 3 |
证明如下:
设四面体ABCD的内切球为球O,球O分别切面BCD、面ACD、面ABD、面ABC于E、F、G、H,
分别设S△BCD、S△ACD、S△ABD、S△ABC为S1、S2、S3、S4
∵球O切平面BCD于点E,
∴OE⊥平面BCD,三棱锥O-BCD的体积为V1=
| 1 |
| 3 |
| 1 |
| 3 |
同理可得:三棱锥O-BCD的体积为V2=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
三棱锥O-ABC的体积为V4=
| 1 |
| 3 |
| 1 |
| 3 |
∴四面体ABCD的体积等于V=V1+V2+V3+V4=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:四面体体积为V=
| 1 |
| 3 |
点评:考查了三角形面积公式和锥体体积公式等知识点,以及用割补的方法求几何体体积的思想.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
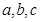 是它的三条边,若
是它的三条边,若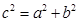 ,则△ABC是直角三角形,然而,若
,则△ABC是直角三角形,然而,若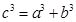 ,则△ABC是锐角三角形,若
,则△ABC是锐角三角形,若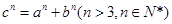 ,则△ABC是( )
,则△ABC是( )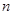 的值确定
的值确定