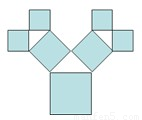
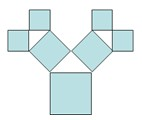
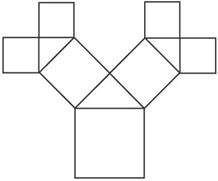
摘要：★如图,正方形上连接等腰直角三角形,直角三角形边上再连接正方形,-,无限重复.设正方形的面积为S1,S2,S3,-,三角形的面积为T1,T2,T3,-,当S1的边长为2时,这些正方形和三角形的面积总和为A.10 B.11 C.12 D.13分析 本题考查无穷等比数列前n项和的极限及运算能力.
网址：http://m.1010jiajiao.com/timu_id_15308[举报]
如图,正方形上连接等腰直角三角形,直角三角形边上再连接正方形,…,无限重复.设正方形的面积为S1,S2,S3,…,三角形的面积为T1,T2,T3,…,当S1的边长为2时,这些正方形和三角形的面积总和为( )
A.10 B
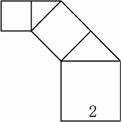
如图所示是毕达哥拉斯的生长程序：正方形上连接着一个等腰直角三角形，等腰直角三角形的直角边上再连接正方形…，如此继续．若共得到1023个正方形，设起始正方形的边长为
| ||
| 2 |
| 1 |
| 32 |
| 1 |
| 32 |
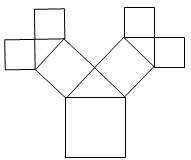如图所示是毕达哥拉斯的生长程序：正方形一边上连接着等腰直角三角形，等腰直角三角形两直角边再分别连接着一个正方形，如此继续下去，共得到127个正方形．若最后得到的正方形的边长为1，则初始正方形的边长为8
8
．
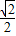，则最小正方形的边长为 ．