题目内容
如图,正方形上连接等腰直角三角形,直角三角形边上再连接正方形,…,无限重复.设正方形的面积为S1,S2,S3,…,三角形的面积为T1,T2,T3,…,当S1的边长为2时,这些正方形和三角形的面积总和为( )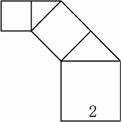
A.10 B
分析：本题考查无穷等比数列前n项和的极限及运算能力.
解：由题意知,正方形的面积{Sn}是首项为4,公比为
的等比数列;三角形的面积{Tn}是首项为1,公比为
的等比数列.
∴S1+S2+…+Sn=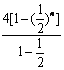
=8［1-(
)n］;
T1+T2+…+Tn=
∴
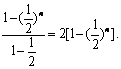
［(S1+S2+…+Sn)+(T1+T2+…+Tn)］
=
8［1-(
)n］+
2［1-(
)n］=10.
答案：A
练习册系列答案
阅读快车系列答案
相关题目
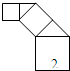如图，正方形上连接等腰直角三角形，直角三角形边上再连接正方形，…，无限重复，设正方形的面积S1，S2，S3，…，三角形的面积为T1，T2，T3，…，当S1的边长为2时，这些正方形和三角形的面积总和为（ ）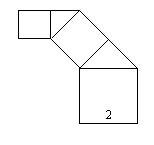
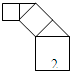如图，正方形上连接等腰直角三角形，直角三角形边上再连接正方形，…，无限重复，设正方形的面积S1，S2，S3，…，三角形的面积为T1，T2，T3，…，当S1的边长为2时，这些正方形和三角形的面积总和为