题目内容
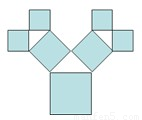
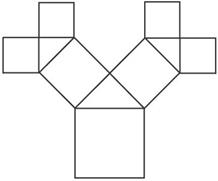
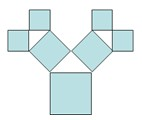 如图所示是毕达哥拉斯的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形…,如此继续.若共得到1023个正方形,设起始正方形的边长为
如图所示是毕达哥拉斯的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形…,如此继续.若共得到1023个正方形,设起始正方形的边长为
| ||
| 2 |
| 1 |
| 32 |
| 1 |
| 32 |
分析:正方形的边长构成以
为首项,以
为公比的等比数列,利用共得到1023个正方形,借助于求和公式,可求得正方形边长变化的次数,从而利用等比数列的通项公式,即可求最小正方形的边长.
| ||
| 2 |
| ||
| 2 |
解答:解:由题意,正方形的边长构成以
为首项,以
为公比的等比数列,现已知共得到1023个正方形,则有
1+2+…+2n=1023,∴n=10
∴最小正方形的边长为
× (
)10-1=
故答案为
| ||
| 2 |
| ||
| 2 |
1+2+…+2n=1023,∴n=10
∴最小正方形的边长为
| ||
| 2 |
| ||
| 2 |
| 1 |
| 32 |
故答案为
| 1 |
| 32 |
点评:本题以图形为载体,考查等比数列的求和公式及通项,关键是的出等比数列模型,正确利用相应的公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
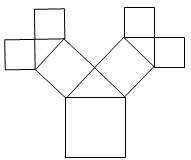 如图所示是毕达哥拉斯的生长程序:正方形一边上连接着等腰直角三角形,等腰直角三角形两直角边再分别连接着一个正方形,如此继续下去,共得到127个正方形.若最后得到的正方形的边长为1,则初始正方形的边长为
如图所示是毕达哥拉斯的生长程序:正方形一边上连接着等腰直角三角形,等腰直角三角形两直角边再分别连接着一个正方形,如此继续下去,共得到127个正方形.若最后得到的正方形的边长为1,则初始正方形的边长为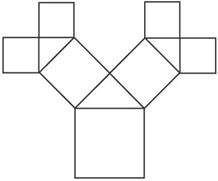
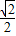 ,则最小正方形的边长为 .
,则最小正方形的边长为 .