摘要:(II) 变形.得
网址:http://m.1010jiajiao.com/timu_id_148910[举报]
(1)选修4-4:矩阵与变换
已知曲线C1:y= 绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,
绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,
(I)求由曲线C1变换到曲线C2对应的矩阵M1;
(II)若矩阵 ,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.
,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.
(2)选修4-4:坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线C: (θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.
(θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.
(3)(选修4-5:不等式选讲)
将12cm长的细铁线截成三条长度分别为a、b、c的线段,
(I)求以a、b、c为长、宽、高的长方体的体积的最大值;
(II)若这三条线段分别围成三个正三角形,求这三个正三角形面积和的最小值.
查看习题详情和答案>>
已知曲线C1:y=
 绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,
绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,(I)求由曲线C1变换到曲线C2对应的矩阵M1;
(II)若矩阵
 ,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.
,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.(2)选修4-4:坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线C:
 (θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.
(θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.(3)(选修4-5:不等式选讲)
将12cm长的细铁线截成三条长度分别为a、b、c的线段,
(I)求以a、b、c为长、宽、高的长方体的体积的最大值;
(II)若这三条线段分别围成三个正三角形,求这三个正三角形面积和的最小值.
查看习题详情和答案>>
(1)选修4-4:矩阵与变换
已知曲线C1:y=
绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,
(I)求由曲线C1变换到曲线C2对应的矩阵M1;
(II)若矩阵M2=
,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.
(2)选修4-4:坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线C:
(θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.
(3)(选修4-5:不等式选讲)
将12cm长的细铁线截成三条长度分别为a、b、c的线段,
(I)求以a、b、c为长、宽、高的长方体的体积的最大值;
(II)若这三条线段分别围成三个正三角形,求这三个正三角形面积和的最小值.
查看习题详情和答案>>
已知曲线C1:y=
| 1 |
| x |
(I)求由曲线C1变换到曲线C2对应的矩阵M1;
(II)若矩阵M2=
|
(2)选修4-4:坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线C:
|
(3)(选修4-5:不等式选讲)
将12cm长的细铁线截成三条长度分别为a、b、c的线段,
(I)求以a、b、c为长、宽、高的长方体的体积的最大值;
(II)若这三条线段分别围成三个正三角形,求这三个正三角形面积和的最小值.
某市的老城区改造建筑用地平面示意图如图所示.经规划调研确定,老城区改造规划建筑用地区域可近似为半径是R的圆面.该圆的内接四边形ABCD是原老城区建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
(I)请计算原老城区建筑用地ABCD的面积及圆面的半径R的值;
(II)因地理条件的限制,边界AD、CD不能变更,而边界AB、BC可以调整.为了提高老城区改造建筑用地的利用率,请在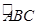 上设计一点P,使得老城区改造的新建筑用地APCD的面积最大,并求出其最大值.
上设计一点P,使得老城区改造的新建筑用地APCD的面积最大,并求出其最大值.

查看习题详情和答案>>
某市的老城区改造建筑用地平面示意图如图所示.经规划调研确定,老城区改造规划建筑用地区域可近似为半径是R的圆面.该圆的内接四边形ABCD是原老城区建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
(I)请计算原老城区建筑用地ABCD的面积及圆面的半径R的值;
(II)因地理条件的限制,边界AD、CD不能变更,而边界AB、BC可以调整.为了提高老城区改造建筑用地的利用率,请在![]() 上设计一点P,使得老城区改造的新建筑用地APCD的面积最大,并求出其最大值.
上设计一点P,使得老城区改造的新建筑用地APCD的面积最大,并求出其最大值.

19.某企业准备投产一批特殊型号的产品,已知该种产品的成本 与产量
与产量 的函数关系式为
的函数关系式为
![]()
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格![]() 与产量
与产量![]() 的函数关系式如下表所示:
的函数关系式如下表所示:
市场情形 | 概率 | 价格 |
好 | 0.4 |
|
中 | 0.4 |
|
差 | 0.2 |
|
设![]() 分别表示市场情形好、中、差时的利润,随机变量
分别表示市场情形好、中、差时的利润,随机变量![]() 表示当产量为
表示当产量为![]() 而市场前景无法确定时的利润.
而市场前景无法确定时的利润.
(I)分别求利润![]() 与产量
与产量![]() 的函数关系式;
的函数关系式;
(II)当产量![]() 确定时,求期望E
确定时,求期望E![]() ;
;
(III)试问产量![]() 取何值时,E
取何值时,E![]() 取得最大值.
取得最大值.