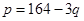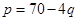题目内容
19.某企业准备投产一批特殊型号的产品,已知该种产品的成本![]()
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格![]() 与产量
与产量![]() 的函数关系式如下表所示:
的函数关系式如下表所示:
市场情形 | 概率 | 价格 |
好 | 0.4 |
|
中 | 0.4 |
|
差 | 0.2 |
|
设![]() 分别表示市场情形好、中、差时的利润,随机变量
分别表示市场情形好、中、差时的利润,随机变量![]() 表示当产量为
表示当产量为![]() 而市场前景无法确定时的利润.
而市场前景无法确定时的利润.
(I)分别求利润![]() 与产量
与产量![]() 的函数关系式;
的函数关系式;
(II)当产量![]() 确定时,求期望E
确定时,求期望E![]() ;
;
(III)试问产量![]() 取何值时,E
取何值时,E![]() 取得最大值.
取得最大值.
(I)解:由题意可得
L1=(164-3q)·q-![]()
=![]()
同理可得L2=-![]() +81q-10(q>0).
+81q-10(q>0).
L3=-![]() +50q-10(q>0).
+50q-10(q>0).
(II)解:由期望定义可知
E![]() =0.4L1+0.4L 2+0.2L3
=0.4L1+0.4L 2+0.2L3
=0.4×(-![]() +144q-10)+0.4×(-
+144q-10)+0.4×(-![]() +81q-10)+0.2×(-
+81q-10)+0.2×(-![]() +50q-10)
+50q-10)
=-![]() +100q-10.
+100q-10.
(III)解:由(II)可知E![]() 是产量q的函数,设
是产量q的函数,设
f(q)= E![]() =-
=-![]() +100q-10(q>0),
+100q-10(q>0),
得![]()
q=10,q=-10(舍去).
由题意及问题的实际意义(或当0<q<10时![]() (q)>0;当q>10时,
(q)>0;当q>10时,![]() (q)<0=可知,当q=10时,f(q)取得最大值,即E
(q)<0=可知,当q=10时,f(q)取得最大值,即E![]() 最大值时的产量q为10.
最大值时的产量q为10.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| q3 |
| 3 |
| 市场情形 | 概率 | 价格p与产量q的函数关系式 |
| 好 | 0.4 | p=164-3q |
| 中 | 0.4 | p=101-3q |
| 差 | 0.2 | p=70-3q |
(Ⅰ)分别求利润L1,L2,L3与产量q的函数关系式;
(Ⅱ)当产量q确定时,求期望Eξq,试问产量q取何值时,Eξq取得最大值.
(07年辽宁卷理)(12分)
某企业准备投产一批特殊型号的产品,已知该种产品的成本![]() 与产量
与产量![]() 的函数关系式为
的函数关系式为
![]()
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格![]() 与产量
与产量![]() 的函数关系式如下表所示:
的函数关系式如下表所示:
市场情形 | 概率 | 价格 |
好 | 0.4 |
|
中 | 0.4 |
|
差 | 0.2 |
|
设![]() 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量![]() ,表示当产量为
,表示当产量为![]() ,而市场前景无法确定的利润.
,而市场前景无法确定的利润.
(I)分别求利润![]() 与产量
与产量![]() 的函数关系式;
的函数关系式;
(II)当产量![]() 确定时,求期望
确定时,求期望![]() ;
;
(III)试问产量![]() 取何值时,
取何值时,![]() 取得最大值.
取得最大值.
(07年辽宁卷理)(12分)
某企业准备投产一批特殊型号的产品,已知该种产品的成本![]() 与产量
与产量![]() 的函数关系式为
的函数关系式为
![]()
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格![]() 与产量
与产量![]() 的函数关系式如下表所示:
的函数关系式如下表所示:
市场情形 | 概率 | 价格 |
好 | 0.4 |
|
中 | 0.4 |
|
差 | 0.2 |
|
设![]() 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量![]() ,表示当产量为
,表示当产量为![]() ,而市场前景无法确定的利润.
,而市场前景无法确定的利润.
(I)分别求利润![]() 与产量
与产量![]() 的函数关系式;
的函数关系式;
(II)当产量![]() 确定时,求期望
确定时,求期望![]() ;
;
(III)试问产量![]() 取何值时,
取何值时,![]() 取得最大值.
取得最大值.
(本小题满分12分)
某企业准备投产一批特殊型号的产品,已知该种产品的成本 与产量
与产量 的函数关系式为
的函数关系式为

该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格 与产量
与产量 的函数关系式如下表所示:
的函数关系式如下表所示:
|
市场情形 |
概率 |
价格 |
|
好 |
0.4 |
|
|
中 |
0.4 |
|
|
差 |
0.2 |
|
设 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量 ,表示当产量为
,表示当产量为 ,而市场前景无法确定的利润.
,而市场前景无法确定的利润.
(I)分别求利润 与产量
与产量 的函数关系式;
的函数关系式;
(II)当产量 确定时,求期望
确定时,求期望 ;
;
(III)试问产量 取何值时,
取何值时, 取得最大值.
取得最大值.