题目内容
(1)选修4-4:矩阵与变换已知曲线C1:y=
 绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,
绕原点逆时针旋转45°后可得到曲线C2:y2-x2=2,(I)求由曲线C1变换到曲线C2对应的矩阵M1;
(II)若矩阵
 ,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.
,求曲线C1依次经过矩阵M1,M2对应的变换T1,T2变换后得到的曲线方程.(2)选修4-4:坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在曲线C:
 (θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.
(θ为参数)上求一点,使它到直线l的距离最小,并求出该点坐标和最小距离.(3)(选修4-5:不等式选讲)
将12cm长的细铁线截成三条长度分别为a、b、c的线段,
(I)求以a、b、c为长、宽、高的长方体的体积的最大值;
(II)若这三条线段分别围成三个正三角形,求这三个正三角形面积和的最小值.
【答案】分析:(1)(I)因为把曲线C1逆时针旋转θ角,得到曲线C2,则旋转变换矩阵为 .
.
(II)先求出依次经过矩阵M1,M2对应的变换T1,T2对应的矩阵,再设曲线C1上任一点经过变换后的对应点坐标,用变换后的坐标表示变换前的坐标,再代入变换前曲线满足的方程,化简即得变换后的曲线方程.
(2)先由直线l的极坐标方程求出直角坐标方程,设出曲线C上任意一点P坐标,用点到直线的距离公式求出点P到直线l的距离,再借助基本正弦函数的最值求出点P到直线l的最小距离.
(3)(I)因为长方体的体积为abc,而a+b+c=12,应用不等式 ,就可求出体积的最大值.
,就可求出体积的最大值.
(II)先把三个正三角形的面积和用S= 表示,因为l+m+n=4,而(l2+m2+n2)(12+12+12)≥(l+m+n)2,所以只需让S乘3再除3即可变形成公式的形式,求出最值.
表示,因为l+m+n=4,而(l2+m2+n2)(12+12+12)≥(l+m+n)2,所以只需让S乘3再除3即可变形成公式的形式,求出最值.
解答:解:(1)(I)∵曲线C1:y= 绕原点逆时针旋转45°后得到曲线C2:y2-x2=2,∴旋转变换矩阵
绕原点逆时针旋转45°后得到曲线C2:y2-x2=2,∴旋转变换矩阵 =
= ;
;
(II)设依次经过矩阵M1,M2对应的变换T1,T2对应的矩阵
任取曲线C1:y= 上的一点P(x,y),它在变换TM作用下变成点P′(x′,y′),则有
上的一点P(x,y),它在变换TM作用下变成点P′(x′,y′),则有 ,即
,即 ,∴
,∴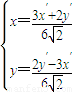
又因为点P在C1:y= 上,得到
上,得到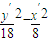 =1即
=1即 =1.
=1.
(2)∵直线l的极坐标方程是ρcosθ+ρsinθ-1=0,∴直角坐标方程是x+y-1=0
设所求的点为P(-1+cosθ,sinθ),则P到直线l的距离d= |
|
当θ+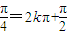 ,k∈Z时,即θ=2kπ+
,k∈Z时,即θ=2kπ+ ,k∈Z,d的最小值为
,k∈Z,d的最小值为 -1
-1
(3)(I)由已知得,a+b+c=12,∴ =64;
=64;
当且仅当a=b=c=4时,等号成立.
(II)设三个正三角形的边长分别为l,m,n,则l+m+n=4
∴这三个正三角形面积和为S=
∴3S= ≥
≥
∴S≥
当且仅当a=b=c=1时,等号成立.
点评:本题(1)主要考查了曲线的旋转变换矩阵的求法以及根据旋转变换求曲线方程,(2)考查了极坐标方程与直角坐标方程的互换,(3)考查了均值不等式和柯西不等式的应用.
 .
.(II)先求出依次经过矩阵M1,M2对应的变换T1,T2对应的矩阵,再设曲线C1上任一点经过变换后的对应点坐标,用变换后的坐标表示变换前的坐标,再代入变换前曲线满足的方程,化简即得变换后的曲线方程.
(2)先由直线l的极坐标方程求出直角坐标方程,设出曲线C上任意一点P坐标,用点到直线的距离公式求出点P到直线l的距离,再借助基本正弦函数的最值求出点P到直线l的最小距离.
(3)(I)因为长方体的体积为abc,而a+b+c=12,应用不等式
 ,就可求出体积的最大值.
,就可求出体积的最大值.(II)先把三个正三角形的面积和用S=
 表示,因为l+m+n=4,而(l2+m2+n2)(12+12+12)≥(l+m+n)2,所以只需让S乘3再除3即可变形成公式的形式,求出最值.
表示,因为l+m+n=4,而(l2+m2+n2)(12+12+12)≥(l+m+n)2,所以只需让S乘3再除3即可变形成公式的形式,求出最值.解答:解:(1)(I)∵曲线C1:y=
 绕原点逆时针旋转45°后得到曲线C2:y2-x2=2,∴旋转变换矩阵
绕原点逆时针旋转45°后得到曲线C2:y2-x2=2,∴旋转变换矩阵 =
= ;
;(II)设依次经过矩阵M1,M2对应的变换T1,T2对应的矩阵

任取曲线C1:y=
 上的一点P(x,y),它在变换TM作用下变成点P′(x′,y′),则有
上的一点P(x,y),它在变换TM作用下变成点P′(x′,y′),则有 ,即
,即 ,∴
,∴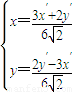
又因为点P在C1:y=
 上,得到
上,得到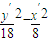 =1即
=1即 =1.
=1.(2)∵直线l的极坐标方程是ρcosθ+ρsinθ-1=0,∴直角坐标方程是x+y-1=0
设所求的点为P(-1+cosθ,sinθ),则P到直线l的距离d=
 |
|当θ+
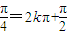 ,k∈Z时,即θ=2kπ+
,k∈Z时,即θ=2kπ+ ,k∈Z,d的最小值为
,k∈Z,d的最小值为 -1
-1
(3)(I)由已知得,a+b+c=12,∴
 =64;
=64;当且仅当a=b=c=4时,等号成立.
(II)设三个正三角形的边长分别为l,m,n,则l+m+n=4
∴这三个正三角形面积和为S=

∴3S=
 ≥
≥
∴S≥

当且仅当a=b=c=1时,等号成立.
点评:本题(1)主要考查了曲线的旋转变换矩阵的求法以及根据旋转变换求曲线方程,(2)考查了极坐标方程与直角坐标方程的互换,(3)考查了均值不等式和柯西不等式的应用.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长. ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积. (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长. ,求证:
,求证: .
.