摘要：解法三:原函数f (x)=log5(x2+1)经过点(2.1).反函数y=g (x)经过点点代入排除A. B.又原函数中y≥1.从而反函数中x≥1.排除 C.故选D. 学科网16 若函数y=log2|ax-1|的图象的对称轴为x=2.则非零实数a的值是( )
网址：http://m.1010jiajiao.com/timu_id_148767[举报]
对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数f（x）的导数，f″（x）是函数f′（x）的导数，f″（x）是函数f（x）的导数，此时，称f″（x）为原函数f（x）的二阶导数．若二阶导数所对应的方程f''（x）=0有实数解x0，则称点（x0，f（x0））为函数f（x）的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．
设三次函数f（x）=2x3-3x2-24x+12请你根据上面探究结果，解答以下问题：
①函数f（x）=2x3-3x2-24x+12的对称中心坐标为
②计算f(
)+f(
)+f(
)+…+f(
)+f(
)=
查看习题详情和答案>>
设三次函数f（x）=2x3-3x2-24x+12请你根据上面探究结果，解答以下问题：
①函数f（x）=2x3-3x2-24x+12的对称中心坐标为
(
，-
)
| 1 |
| 2 |
| 1 |
| 2 |
(
，-
)
；| 1 |
| 2 |
| 1 |
| 2 |
②计算f(
| 1 |
| 2013 |
| 2 |
| 2013 |
| 3 |
| 2013 |
| 2012 |
| 2013 |
| 2013 |
| 2013 |
-1019
-1019
．对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数f（x）的导数，f″（x）是函数f′（x）的导数，f″（x）是函数f（x）的导数，此时，称f″（x）为原函数f（x）的二阶导数．若二阶导数所对应的方程f''（x）=0有实数解x0，则称点（x0，f（x0））为函数f（x）的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．
设三次函数f（x）=2x3-3x2-24x+12请你根据上面探究结果，解答以下问题：
①函数f（x）=2x3-3x2-24x+12的对称中心坐标为______；
②计算f(
)+f(
)+f(
)+…+f(
)+f(
)=______．
查看习题详情和答案>>
设三次函数f（x）=2x3-3x2-24x+12请你根据上面探究结果，解答以下问题：
①函数f（x）=2x3-3x2-24x+12的对称中心坐标为______；
②计算f(
| 1 |
| 2013 |
| 2 |
| 2013 |
| 3 |
| 2013 |
| 2012 |
| 2013 |
| 2013 |
| 2013 |
对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数f（x）的导数，f″（x）是函数f′（x）的导数，f″（x）是函数f（x）的导数，此时，称f″（x）为原函数f（x）的二阶导数．若二阶导数所对应的方程f''（x）=0有实数解x，则称点（x，f（x））为函数f（x）的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．
设三次函数f（x）=2x3-3x2-24x+12请你根据上面探究结果，解答以下问题：
①函数f（x）=2x3-3x2-24x+12的对称中心坐标为 ；
②计算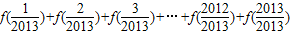
= ．
查看习题详情和答案>>
设三次函数f（x）=2x3-3x2-24x+12请你根据上面探究结果，解答以下问题：
①函数f（x）=2x3-3x2-24x+12的对称中心坐标为 ；
②计算
= ．
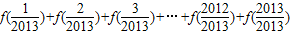查看习题详情和答案>>
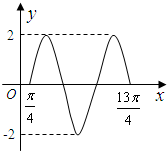（2012•济南三模）函数f（x）=2sin（ωx+φ）的图象，其部分图象如图所示，则f（0）=