题目内容
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数f(x)的导数,f″(x)是函数f′(x)的导数,f″(x)是函数f(x)的导数,此时,称f″(x)为原函数f(x)的二阶导数.若二阶导数所对应的方程f''(x)=0有实数解x,则称点(x,f(x))为函数f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设三次函数f(x)=2x3-3x2-24x+12请你根据上面探究结果,解答以下问题:
①函数f(x)=2x3-3x2-24x+12的对称中心坐标为 ;
②计算
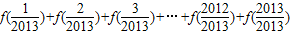 = .
= .
【答案】分析:①求出所给函数的二阶导数,由二阶导数等于0求出x的值,代入原函数求出对称中心;
②利用对称中心坐标得到前2012项的和,在求出f(1)的值,则答案可求.
解答:解:①由f(x)=2x3-3x2-24x+12,得f′=6x2-6x-24,f′′(x)=12x-6.
由f′′(x)=12x-6=0,得x= .
. .
.
所以函数f(x)=2x3-3x2-24x+12的对称中心坐标为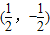 .
.
故答案为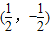 .
.
②因为函数f(x)=2x3-3x2-24x+12的对称中心坐标为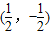 .
.
所以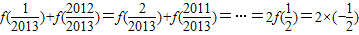 =-1.
=-1.
由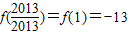 .
.
所以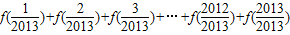 =-1006-13=-1019.
=-1006-13=-1019.
故答案为-1019.
点评:本题考查了简单的演绎推理,是新定义题,解答的关键是利用对称中心求值,是中档题.
②利用对称中心坐标得到前2012项的和,在求出f(1)的值,则答案可求.
解答:解:①由f(x)=2x3-3x2-24x+12,得f′=6x2-6x-24,f′′(x)=12x-6.
由f′′(x)=12x-6=0,得x=
 .
. .
.所以函数f(x)=2x3-3x2-24x+12的对称中心坐标为
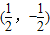 .
.故答案为
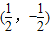 .
.②因为函数f(x)=2x3-3x2-24x+12的对称中心坐标为
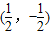 .
.所以
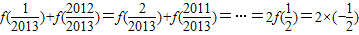 =-1.
=-1.由
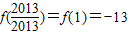 .
.所以
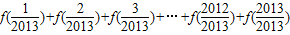 =-1006-13=-1019.
=-1006-13=-1019.故答案为-1019.
点评:本题考查了简单的演绎推理,是新定义题,解答的关键是利用对称中心求值,是中档题.

练习册系列答案
相关题目