网址:http://m.1010jiajiao.com/timu_id_14745[举报]

(Ⅰ)求该运动员两次都命中7环的概率;
(Ⅱ)求ξ的分布列;
(Ⅲ)求ξ的数学期望Eξ。
(12分)甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
射手甲 |
| 射手乙 | ||||||
环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 | |
概率 |
|
|
| 概率 |
|
|
| |
(I)若甲射手共有5发子弹,一旦命中10环就停止射击,求他剩余3颗子弹的概率;
(Ⅱ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅲ)若两个射手各射击1次,记所得的环数之和为![]() ,求
,求![]() 的分布列和期望。
的分布列和期望。
从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
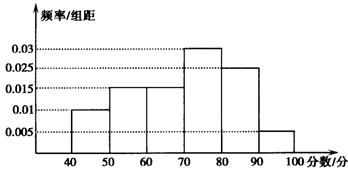
⑴80~90这一组的频数、频率分别是多少?
⑵估计这次环保知识竞赛的及格率(60分及以上为及格). (本小题满分10分)
【解析】本试题主要考查了统计和概率的综合运用。
第一问频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
第二问0.015×10+0.025×10+0.03×10+0.005×10=0.75
解:(1)频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
(2)0.015×10+0.025×10+0.03×10+0.005×10=0.75
查看习题详情和答案>>
(本小题满分13分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:K^S*5U.C#O%
|
射手甲 |
射手乙 |
||||||
|
环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
|
概率 |
|
|
|
概率 |
|
|
|
(1)若甲射手共有5发子弹,一旦命中10环就停止射击,求他剩余3颗子弹的概率;
(2)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;K^S*5U.C#O%
(3)若两个射手各射击1次,记所得的环数之和为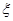 ,求
,求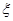 的分布列和期望。
的分布列和期望。
查看习题详情和答案>>
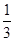
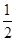
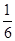
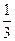

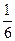
 ,求
,求