摘要：设数列{an}的前n项和为Sn.满足an+1＝Sn-3n.(1)当a1＝1时.用n表示Sn,(2)求首项a1的取值范围.使{an}是递减数列.
网址：http://m.1010jiajiao.com/timu_id_147052[举报]
（本小题满分12分）
数列{an}的前n项和为Sn，且a1=a，Sn+1=2Sn+n+1，n∈N*
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）当a=1时，若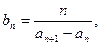
设数列{bn}的前n项和Tn，n∈N*，证明Tn＜2。
（本小题满分12分）
数列{an}的前n项和为Sn，且a1=a，Sn+1=2Sn+n+1，n∈N*
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）当a=1时，若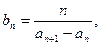
设数列{bn}的前n项和Tn，n∈N*，证明Tn＜2。
数列{an}的前n项和为Sn，且a1=a，Sn+1=2Sn+n+1，n∈N*
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）当a=1时，若
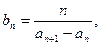设数列{bn}的前n项和Tn，n∈N*，证明Tn＜2。(本小题满分12分)
设{an}是公差不为O的等差数列，Sn是其前n项和，已知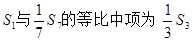
，且
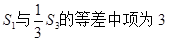
(1)求数列{an}的通项an
(2)求等比数列{bn}满足b1=S1 ,b2=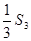
, 求和Tn=a1b1+a2b2+…+anbn
查看习题详情和答案>>
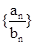的前n项和Sn.
，且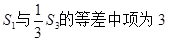
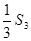, 求和Tn=a1b1+a2b2+…+anbn