题目内容
(本小题满分12分) 设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(1)求{an},{bn}的通项公式;
(2)求数列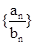 的前n项和Sn.
的前n项和Sn.
【答案】
(1) an=2n-1 ,bn=2n-1.(2) 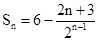
【解析】(1) 设等差数列的公差为d 等比数列的公比为q,然后根据a1=b1=1,a3+b5=21,a5+b3=13.可建立关于d和q的两个方程,求出d,q的值,从而得到{an},{bn}的通项公式.
(2)由(1)知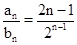 ,显然要采用错位相减的方法求和.
,显然要采用错位相减的方法求和.
(1)设等差数列的公差为d 等比数列的公比为q,
由题意得 1+2d+q4=21, ① 1+4d+q2=13, ②
①×2-②得,2q4-q2-28=0,解得q2=4 又由题意,知{bn}各项为正,
所以q=2,代入②得d=2, 所以an=2n-1 ,bn=2n-1.
(2)由(1)可知,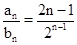 ,
,
又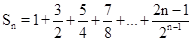 , (1)
, (1)
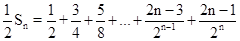 , (2)
, (2)
(2)-(1)得 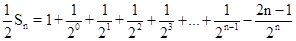
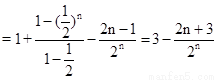 ,∴
,∴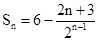

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目