摘要:的条件下.设.问是否存在最大的整数m.使得对任意.均有若存在.求出的值.若不存在.说明理由.
网址:http://m.1010jiajiao.com/timu_id_13572[举报]
 已知:如图,抛物线y=x2+bx+c(b、c为常数)经过原点和E(3,0).
已知:如图,抛物线y=x2+bx+c(b、c为常数)经过原点和E(3,0).(1)求该抛物线所对应的函数关系式;
(2)设A是该抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值及此时点A的坐标;如果不存在,请说明理由;
③当B(
| 1 | 2 |
如图,在平面直角坐标系中,直线 与x轴、y轴分别交于点B、C;抛物线y=-x2+bx+c经过B、C两点,并与x轴交于另一点A.
与x轴、y轴分别交于点B、C;抛物线y=-x2+bx+c经过B、C两点,并与x轴交于另一点A.
(1)求该抛物线所对应的函数关系式;
(2)设P(x,y)是在第一象限内该抛物线上的一个动点,过点P作直线l⊥x轴于点M,交直线BC于点N.
①试问:线段PN的长度是否存在最大值?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;
②当x=______时,P、C、O、N四点能围成平行四边形.
(3)连接PC,在(2)的条件下,解答下列问题:
①请用含x的式子表示线段BN的长度:BN=______;
②若PC⊥BC,试求出此时点M的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
 与x轴、y轴分别交于点B、C;抛物线y=-x2+bx+c经过B、C两点,并与x轴交于另一点A.
与x轴、y轴分别交于点B、C;抛物线y=-x2+bx+c经过B、C两点,并与x轴交于另一点A.(1)求该抛物线所对应的函数关系式;
(2)设P(x,y)是在第一象限内该抛物线上的一个动点,过点P作直线l⊥x轴于点M,交直线BC于点N.
①试问:线段PN的长度是否存在最大值?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;
②当x=______时,P、C、O、N四点能围成平行四边形.
(3)连接PC,在(2)的条件下,解答下列问题:
①请用含x的式子表示线段BN的长度:BN=______;
②若PC⊥BC,试求出此时点M的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
如图,在平面直角坐标系中,直线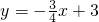 与x轴、y轴分别交于点B、C;抛物线y
与x轴、y轴分别交于点B、C;抛物线y =-x2+bx+c经过B、C两点,并与x轴交于另一点A.
=-x2+bx+c经过B、C两点,并与x轴交于另一点A.
(1)求该抛物线所对应的函数关系式;
(2)设P(x,y)是在第一象限内该抛物线上的一个动点,过点P作直线l⊥x轴于点M,交直线BC于点N.
①试问:线段PN的长度是否存在最大值?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;
②当x=______时,P、C、O、N四点能围成平行四边形.
(3)连接PC,在(2)的条件下,解答下列问题:
①请用含x的式子表示线段BN的长度:BN=______;
②若PC⊥BC,试求出此时点M的坐标.
查看习题详情和答案>>
已知:如图,抛物线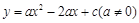 与
与 轴交于点
轴交于点 ,与
,与 轴交于点A、B,点A的坐标为(4,0)
轴交于点A、B,点A的坐标为(4,0)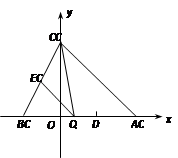
【小题1】求该抛物线的解析式;
【小题2】点Q是线段AB上的动点,过点Q作QE//AC,交BC于点E,连接CQ,设△CQE的面积为S,Q(m,0),试求S与m之间的函数关系式(写出自变量m的取值范围);
【小题3】在(2)的条件下,当△CQE的面积最大时,求点E的坐标.
【小题4】若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0). 问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标,若不存在,请说明理由.
(2012•孝感模拟)如图,在平面直角坐标系中,直线y=-
x+3与x轴、y轴分别交于点B、C;抛物线y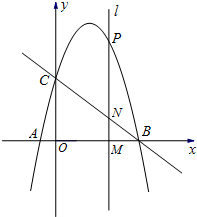 =-x2+bx+c经过B、C两点,并与x轴交于另一点A.
=-x2+bx+c经过B、C两点,并与x轴交于另一点A.
(1)求该抛物线所对应的函数关系式;
(2)设P(x,y)是在第一象限内该抛物线上的一个动点,过点P作直线l⊥x轴于点M,交直线BC于点N.
①试问:线段PN的长度是否存在最大值?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;
②当x=
(3)连接PC,在(2)的条件下,解答下列问题:
①请用含x的式子表示线段BN的长度:BN=
②若PC⊥BC,试求出此时点M的坐标.
查看习题详情和答案>>
| 3 |
| 4 |
 =-x2+bx+c经过B、C两点,并与x轴交于另一点A.
=-x2+bx+c经过B、C两点,并与x轴交于另一点A.(1)求该抛物线所对应的函数关系式;
(2)设P(x,y)是在第一象限内该抛物线上的一个动点,过点P作直线l⊥x轴于点M,交直线BC于点N.
①试问:线段PN的长度是否存在最大值?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;
②当x=
1或3
1或3
时,P、C、O、N四点能围成平行四边形.(3)连接PC,在(2)的条件下,解答下列问题:
①请用含x的式子表示线段BN的长度:BN=
5-
x
| 5 |
| 4 |
5-
x
;| 5 |
| 4 |
②若PC⊥BC,试求出此时点M的坐标.