��Ŀ����
��2012•Т��ģ�⣩��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-
x+3��x�ᡢy��ֱ��ڵ�B��C��������y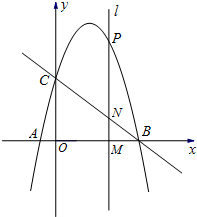 =-x2+bx+c����B��C���㣬����x�ύ����һ��A��
=-x2+bx+c����B��C���㣬����x�ύ����һ��A��
��1���������������Ӧ�ĺ�����ϵʽ��
��2����P��x��y�����ڵ�һ�����ڸ��������ϵ�һ�����㣬����P��ֱ��l��x���ڵ�M����ֱ��BC�ڵ�N��
�����ʣ��߶�PN�ij����Ƿ�������ֵ�������ڣ�����������ֵ����ʱx��ֵ���������ڣ���˵�����ɣ�
�ڵ�x=
��3������PC���ڣ�2���������£�����������⣺
�����ú�x��ʽ�ӱ�ʾ�߶�BN�ij��ȣ�BN=
����PC��BC���������ʱ��M�����꣮
| 3 |
| 4 |
 =-x2+bx+c����B��C���㣬����x�ύ����һ��A��
=-x2+bx+c����B��C���㣬����x�ύ����һ��A����1���������������Ӧ�ĺ�����ϵʽ��
��2����P��x��y�����ڵ�һ�����ڸ��������ϵ�һ�����㣬����P��ֱ��l��x���ڵ�M����ֱ��BC�ڵ�N��
�����ʣ��߶�PN�ij����Ƿ�������ֵ�������ڣ�����������ֵ����ʱx��ֵ���������ڣ���˵�����ɣ�
�ڵ�x=
1��3
1��3
ʱ��P��C��O��N�ĵ���Χ��ƽ���ı��Σ���3������PC���ڣ�2���������£�����������⣺
�����ú�x��ʽ�ӱ�ʾ�߶�BN�ij��ȣ�BN=
5-
x
| 5 |
| 4 |
5-
x
��| 5 |
| 4 |
����PC��BC���������ʱ��M�����꣮
��������1������һ�κ��������B��C�����꣬Ȼ�����ô���ϵ���������κ�������ʽ���ɣ�
��2���ٸ��ݶ��κ�������ʽ�����P�����꣬����ֱ��BC����ʽ�����N�����꣬Ȼ�����PN=PM-NM���ɵó�PN�ı���ʽ�������䷽����������ֵ��
�ڸ���PN��OC���ɵó�ҪʹPCONΧ��ƽ���ı��Σ���PN=CO����Ϣ�PN�ı���ʽ�ɽ������̣�������ɵó��𰸣�
��3���ٸ��ݡ�BNM�ס�BCO���������������εĶ�Ӧ�߳ɱ����ɵó�BN�Ĺ���x�ı���ʽ��
�����жϳ���PCN�ס�BOC��Ȼ���������ö�Ӧ�߳ɱ����ɵó����̣�������ɵó�x��ֵ��Ҳ��ȷ����M�����꣮
��2���ٸ��ݶ��κ�������ʽ�����P�����꣬����ֱ��BC����ʽ�����N�����꣬Ȼ�����PN=PM-NM���ɵó�PN�ı���ʽ�������䷽����������ֵ��
�ڸ���PN��OC���ɵó�ҪʹPCONΧ��ƽ���ı��Σ���PN=CO����Ϣ�PN�ı���ʽ�ɽ������̣�������ɵó��𰸣�
��3���ٸ��ݡ�BNM�ס�BCO���������������εĶ�Ӧ�߳ɱ����ɵó�BN�Ĺ���x�ı���ʽ��
�����жϳ���PCN�ס�BOC��Ȼ���������ö�Ӧ�߳ɱ����ɵó����̣�������ɵó�x��ֵ��Ҳ��ȷ����M�����꣮
����⣺��1������ֱ��y=-
x+3����B��C���㣬��y=0��x=4����x=0����y=3��
�ʿɵã�B��4��0����C��0��3����
�ߵ�B��C��������y=-x2+bx+c�ϣ����ǵ�
��
��ã�b=
��c=3��
����������ϵʽΪy=-x2+
x+3��
��2���١ߵ�P��x��y����������y=-x2+
x+3�ϣ���PN��x�ᣬ
�����P��������x��-x2+
x+3��ͬ�������N������Ϊ��x��-
x+3����
�֡ߵ�P�ڵ�һ���ޣ�
��PN=PM-NM=��-x2+
x+3��-��-
x+3��=-x2+4x=-��x-2��2+4��
�൱x=2ʱ��
�߶�PN�ij��ȵ����ֵΪ4��
����ΪPN��CO��ҪʹPCONΧ��ƽ���ı��Σ���PN=CO��
�ɢٵã�PN=-x2+4x���ʿɵã�-x2+4x=3��
��ã�x=1��3��
��3��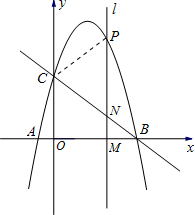 �١ߡ�BNM�ס�BCO��
�١ߡ�BNM�ס�BCO��
��
=
����
=
��
��ã�BN=5-
x��
����PC��BC�á�PCN=��COB=90�㣬
�֡ߡ�PNC=��OCB����PN��OC�ó�����
���PCN�ס�BOC��
��
=
����
=
��
��ã�x=
��x=0����ȥ����
�ʴ�ʱ��M������Ϊ��
��0����
| 3 |
| 4 |
�ʿɵã�B��4��0����C��0��3����
�ߵ�B��C��������y=-x2+bx+c�ϣ����ǵ�
|
��ã�b=
| 13 |
| 4 |
����������ϵʽΪy=-x2+
| 13 |
| 4 |
��2���١ߵ�P��x��y����������y=-x2+
| 13 |
| 4 |
�����P��������x��-x2+
| 13 |
| 4 |
| 3 |
| 4 |
�֡ߵ�P�ڵ�һ���ޣ�
��PN=PM-NM=��-x2+
| 13 |
| 4 |
| 3 |
| 4 |
�൱x=2ʱ��
�߶�PN�ij��ȵ����ֵΪ4��
����ΪPN��CO��ҪʹPCONΧ��ƽ���ı��Σ���PN=CO��
�ɢٵã�PN=-x2+4x���ʿɵã�-x2+4x=3��
��ã�x=1��3��
��3��
 �١ߡ�BNM�ס�BCO��
�١ߡ�BNM�ס�BCO����
| MN |
| OC |
| BN |
| BC |
-
| ||
| 3 |
| BN |
| 5 |
��ã�BN=5-
| 5 |
| 4 |
����PC��BC�á�PCN=��COB=90�㣬
�֡ߡ�PNC=��OCB����PN��OC�ó�����
���PCN�ס�BOC��
��
| PN |
| BC |
| CN |
| OC |
| -x2+4x |
| 5 |
| ||
| 3 |
��ã�x=
| 23 |
| 12 |
�ʴ�ʱ��M������Ϊ��
| 23 |
| 12 |
�������������ڶ��κ������ۺ���Ŀ���漰�����������ε��ж������ʡ�ƽ���ı��ε����ʣ��������Ҫ������������֪ʶ������ݣ�����̽����Ŀ����������

��ϰ��ϵ�д�
 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
�����Ŀ
 ��2012•Т��ģ�⣩��ͼ��ֱ��AB��CD�ཻ�ڵ�E��EF��AB��E������CEF=59�㣬���AED�Ķ���Ϊ
��2012•Т��ģ�⣩��ͼ��ֱ��AB��CD�ཻ�ڵ�E��EF��AB��E������CEF=59�㣬���AED�Ķ���Ϊ