摘要:21.已知椭圆中心在原点.焦点在坐标轴上.直线与椭圆在第一象限内的交点是.点在轴上的射影恰好是椭圆的右焦点.另一个焦点是.且.(1)求椭圆的方程,(2)直线过点.且与椭圆交于两点.求的内切圆面积的最大值.
网址:http://m.1010jiajiao.com/timu_id_135712[举报]
(本题满分12分)已知椭圆中心在原点,焦点在x轴上,离心率![]() ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为![]() (1)求椭圆的标准方程;(2)已知直线L与椭圆相交于P、Q两点,O为原点,且OP⊥OQ。试探究点O到直线L的距离是否为定值?若是,求出这个定值;若不是,说明理由。
(1)求椭圆的标准方程;(2)已知直线L与椭圆相交于P、Q两点,O为原点,且OP⊥OQ。试探究点O到直线L的距离是否为定值?若是,求出这个定值;若不是,说明理由。
(本题满分12分)已知椭圆中心在原点,焦点在x轴上,离心率 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为 (1)求椭圆的标准方程;(2)已知直线L与椭圆相交于P、Q两点,O为原点,且OP⊥OQ。试探究点O到直线L的距离是否为定值?若是,求出这个定值;若不是,说明理由。
(1)求椭圆的标准方程;(2)已知直线L与椭圆相交于P、Q两点,O为原点,且OP⊥OQ。试探究点O到直线L的距离是否为定值?若是,求出这个定值;若不是,说明理由。
 ,过椭圆的右焦点且垂直于长轴的弦长为
,过椭圆的右焦点且垂直于长轴的弦长为 (1)求椭圆的标准方程;(2)已知直线L与椭圆相交于P、Q两点,O为原点,且OP⊥OQ。试探究点O到直线L的距离是否为定值?若是,求出这个定值;若不是,说明理由。
(1)求椭圆的标准方程;(2)已知直线L与椭圆相交于P、Q两点,O为原点,且OP⊥OQ。试探究点O到直线L的距离是否为定值?若是,求出这个定值;若不是,说明理由。 (本题满分12分)已知椭圆E:
(本题满分12分)已知椭圆E:![]() (其中
(其中![]() ),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线
),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线![]() 分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
(Ⅰ)若直线L在![]() 轴上的截距为
轴上的截距为![]() ,求证: 直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若
,求证: 直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若![]() 的最大值为1200,求椭圆E的方程.
的最大值为1200,求椭圆E的方程.
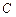 :
: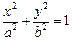 (
(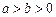 )的离心率
)的离心率 ,左、右焦点分别为
,左、右焦点分别为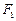 、
、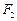 ,点
,点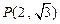 满足:
满足: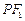 的中垂线上.
的中垂线上. (
(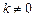 )的直线
)的直线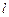 与
与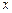 轴、椭圆
轴、椭圆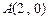 、
、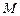 、
、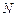 ,且
,且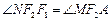 ,求
,求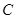 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆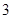 ,最小值为
,最小值为 .
.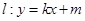 与椭圆
与椭圆 两点(
两点( 为直径的圆过椭圆
为直径的圆过椭圆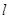 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.