题目内容
 (本题满分12分)已知椭圆E:
(本题满分12分)已知椭圆E:![]() (其中
(其中![]() ),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线
),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线![]() 分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
(Ⅰ)若直线L在![]() 轴上的截距为
轴上的截距为![]() ,求证: 直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若
,求证: 直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若![]() 的最大值为1200,求椭圆E的方程.
的最大值为1200,求椭圆E的方程.
(Ⅰ) 见解析 (Ⅱ) ![]()
解析:
法一:(1)设T(x0,y0),由对称性,不妨设![]() ,∴
,∴![]() ,∴
,∴![]() 且
且![]() ;
;
∵直线L椭圆E只有一个公共点T,由椭圆E:![]()
![]() 得
得![]() ,求导
,求导
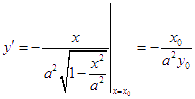 ,∴直线L:
,∴直线L:![]() ,得
,得![]() ;
;
∵直线L在![]() 轴上的截距为
轴上的截距为![]() ,令
,令![]() ,得
,得![]() ,∴
,∴![]() ;
;
∴直线L斜率的绝对值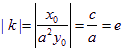 ;
;
(2)直线L:![]() 与
与![]() 的交点
的交点![]() ,
,
设![]() ,在RTDF1AF2和RTDF1BF2中,
,在RTDF1AF2和RTDF1BF2中,
![]() ,当
,当![]() 时,
时,

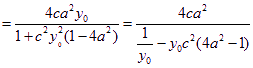 ;
;
∵![]() 且
且![]() ,∴
,∴![]() ,
,
∵![]() 最大值为1200,只需令
最大值为1200,只需令![]() ,
,
∴![]() ,∴
,∴![]() ;∴
;∴![]() ∴椭圆E的方程为
∴椭圆E的方程为![]() .
.
解法二:(1)依题意设直线L:![]() ,代入椭圆E:
,代入椭圆E:![]() 整理得:
整理得:
![]() (*),∵直线L椭圆E只有一个公共点T,
(*),∵直线L椭圆E只有一个公共点T,
∴方程(*)的![]() ,
,
整理得:![]() ,①∵直线L在
,①∵直线L在![]() 轴上的截距为
轴上的截距为![]() ,∴
,∴![]() 代入①得
代入①得![]() ,∴
,∴![]() ;
;
(2)考虑对称性,不妨设![]() ,由①得
,由①得![]() ,直线L:
,直线L:![]() 与
与![]() 的交点
的交点![]() ,设
,设![]() ,在RTDF1AF2和RTDF1BF2中,
,在RTDF1AF2和RTDF1BF2中,![]() ,由①得
,由①得![]() ,
,
当![]() 时,
时,![]()
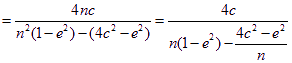 ,∵
,∵![]() 且
且![]() ,
,
∴![]() ,
,
∵![]() 最大值为1200,只需令
最大值为1200,只需令![]() ,∴
,∴![]() ;
;
∴![]() ∴椭圆E的方程为
∴椭圆E的方程为![]() .
.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围