网址:http://m.1010jiajiao.com/timu_id_13559[举报]
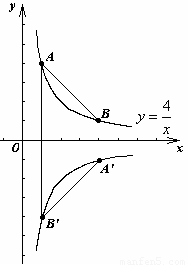
在平面直角坐标系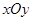 中,A、B为反比例函数
中,A、B为反比例函数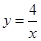
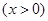 的图象上两点,A点的横坐标与B点的纵坐标均为1,将
的图象上两点,A点的横坐标与B点的纵坐标均为1,将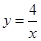
 的图象绕原点O顺时针旋转90°,A点的对应点为
的图象绕原点O顺时针旋转90°,A点的对应点为 ,B点的对应点为
,B点的对应点为 .
.
(1)求旋转后的图象解析式;
(2)求 、
、 点的坐标;
点的坐标;
(3)连结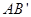 .动点
.动点 从
从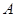 点出发沿线段
点出发沿线段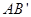 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点 运动;动点
运动;动点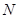 同时从
同时从 点出发沿线段
点出发沿线段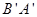 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点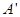 运动,当其中一个点停止运动时另一个点也随之停止运动.设运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设运动的时间为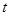 秒,试探究:是否存在使
秒,试探究:是否存在使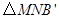 为等腰直角三角形的
为等腰直角三角形的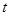 值,若存在,求出
值,若存在,求出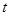 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看习题详情和答案>>
问题背景
若矩形的周长为1,则可求出该矩形面积的最大值.我们可以设矩形的一边长为x,面积为s,则s与x的函数关系式为:  ,利用函数的图象或通过配方均可求得该函数的最大值.
,利用函数的图象或通过配方均可求得该函数的最大值.
提出新问题
若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的一边长为x,周长为y,则y与x的函数关系式为: ,问题就转化为研究该函数的最大(小)值了.
,问题就转化为研究该函数的最大(小)值了.
解决问题
借鉴我们已有的研究函数的经验,探索函数 的最大(小)值.
的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数 的图象:
的图象:
|
x |
··· |
|
|
|
1 |
2 |
3 |
4 |
··· |
|
y |
|
|
|
|
|
|
|
|
|

(2)观察猜想:观察该函数的图象,猜想当x= 时,函数 有最 值(填
有最 值(填
“大”或“小”),是 .
(3)推理论证:问题背景中提到,通过配方可求二次函数 的最大值,请你尝试通过配方求函数
的最大值,请你尝试通过配方求函数 的最大(小)值,以证明你的猜想. 〔提示:当
的最大(小)值,以证明你的猜想. 〔提示:当 时,
时, 〕
〕
查看习题详情和答案>>
阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
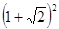 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设
 (其中
(其中 均为整数),则有
均为整数),则有
 . ∴
. ∴ ,
, .
.
这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当 均为正整数时,若
均为正整数时,若
 ,用含
,用含 的式子分别表示
的式子分别表示 ,得
,得 =_ ,
=_ , =_ ;
=_ ;
(2)利用上面结论,找一组正整数 ,填空_ +_ =(_ +_ )
,填空_ +_ =(_ +_ ) ;
;
(3)若
 ,且
,且 均为正整数,求a的值.
均为正整数,求a的值.



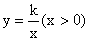 的图象经过点B.
的图象经过点B.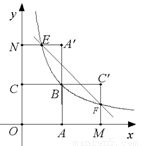
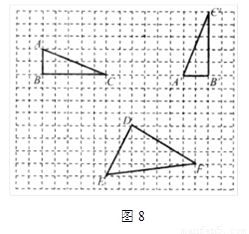
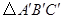 是由格点
是由格点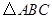 通过怎样变换得到的?
通过怎样变换得到的?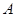 的坐标为(
的坐标为(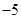 ,
,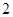 ),点
),点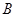 的坐标为
的坐标为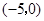 ,请求出过
,请求出过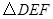 各顶点的坐标.
各顶点的坐标.