题目内容
在平面直角坐标系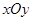 中,A、B为反比例函数
中,A、B为反比例函数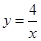
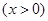 的图象上两点,A点的横坐标与B点的纵坐标均为1,将
的图象上两点,A点的横坐标与B点的纵坐标均为1,将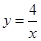
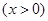 的图象绕原点O顺时针旋转90°,A点的对应点为
的图象绕原点O顺时针旋转90°,A点的对应点为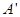 ,B点的对应点为
,B点的对应点为 .
.
(1)求旋转后的图象解析式;
(2)求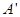 、
、 点的坐标;
点的坐标;
(3)连结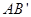 .动点
.动点 从
从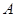 点出发沿线段
点出发沿线段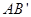 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点 运动;动点
运动;动点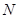 同时从
同时从 点出发沿线段
点出发沿线段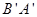 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点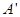 运动,当其中一个点停止运动时另一个点也随之停止运动.设运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设运动的时间为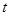 秒,试探究:是否存在使
秒,试探究:是否存在使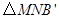 为等腰直角三角形的
为等腰直角三角形的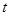 值,若存在,求出
值,若存在,求出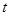 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1)旋转后的图象解析式为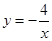
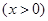 .
.
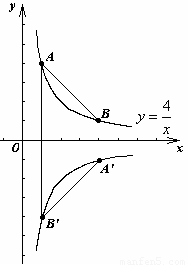
(2)由旋转可得 (4,-1)、
(4,-1)、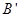 (1,-4).
(1,-4).
(3)依题意,可知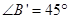 .若
.若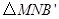 为直角三角形,则
为直角三角形,则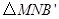 同时也是等腰三角形,因此,只需求使
同时也是等腰三角形,因此,只需求使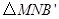 为直角三角形的
为直角三角形的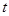 值.
值.
分两种情况讨论:
① 当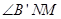 是直角,
是直角, 时,如图1,
时,如图1,

∵AB′=8,B′A′== ,AM=B′N=MN=t,
,AM=B′N=MN=t,
∴B′M=8-t,
∵ ,
,
∴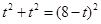 .
.
解得 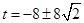 (舍去负值),
(舍去负值),
∴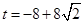 .
.
②当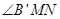 是直角,
是直角,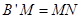 时,
时,
如图2,
∵AB′=8,B′A′== ,AM=B′N=t,
,AM=B′N=t,
∴B′M=MN=8-t,
∵ ,
,
∴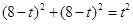 ,
,
解得  .
.
∵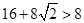 ,
,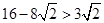 ,
,
∴此时t值不存在.
(此类情况不计算,通过画图说明t值不存在也可以)
综上所述,当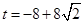 时,
时,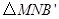 为等腰直角三角形.
为等腰直角三角形.
【解析】(1)首先把x=1代入反比例函数y=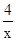 (x>0)的解析式,求出对应的y值,得到A点坐标,然后由旋转的性质得出∠AOA′=90°,OA=OA′,如果分别过A、A′作AM⊥y轴于M,A′N⊥x轴于N,连接OA,OA′,易证△OAM≌△OA′N,得到A′的坐标,从而求出旋转后的图象解析式;
(x>0)的解析式,求出对应的y值,得到A点坐标,然后由旋转的性质得出∠AOA′=90°,OA=OA′,如果分别过A、A′作AM⊥y轴于M,A′N⊥x轴于N,连接OA,OA′,易证△OAM≌△OA′N,得到A′的坐标,从而求出旋转后的图象解析式;
(2)上问已经求出A′的坐标,同样求出点B′的坐标;
(3)首先运用待定系数法求出直线A′B′的解析式,由斜率k的值可知∠A′B′A=45°.然后假设存在使△MNB'为等腰直角三角形的t值,那么分两种情况讨论:①∠B′NM=90°;②∠B′MN=90°.针对每一种情况,都可以利用等腰直角三角形中斜边是直角边的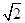 倍列出方程,从而求出结果.
倍列出方程,从而求出结果.

 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.